陰関数のグラフの概形の例題です。
\(y=f(x)\) の形にできるなら、微分してグラフを書くことができます。
また、対称性にも気を付けます。
(例題)
曲線 \(y^2=x^3-ax^2\)
について、次の\(a\)の値におけるグラフの概形をそれぞれ描け。(凹凸も調べよ)
(1)\(a=0\) (2)\(a=-3\) (3)\(a=3\)
また、\(y^2=(-y)^2\) なのでこの曲線は\(x\)軸対称です。
(解答)
(1)
曲線 \(y^2=x^3\)・・・①
\(x^3≧0\) より、定義域は \(x≧0\)
このとき①より
\(y=±\sqrt{x^3}\)
\(y=\sqrt{x^3}\) について考えると
\(y’=\displaystyle\frac{3}{2}\sqrt{x}\ (>0)\)
\(y”=\displaystyle\frac{3}{4\sqrt{x}}\ (>0)\)
(単調増加、下に凸)
よって、\(y=-\sqrt{x^3}\) のグラフは、\(y=\sqrt{x^3}\) のグラフと\(x\)軸対称だから、曲線①のグラフは次の通り。
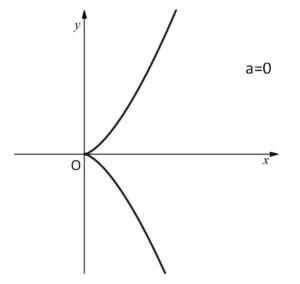
(2)
曲線 \(y^2=x^3+3x^2\)・・・②
\(y^2=x^2(x+3)\)
\(x^2(x+3)≧0\) より、定義域は \(x≧-3\)
このとき②より
\(y=±\sqrt{x^3+3x^2}\)
\(y=\sqrt{x^3+3x^2}\) について
\(y’=\displaystyle\frac{3x^2+6x}{2\sqrt{x^3+3x^2}}=\displaystyle\frac{3x(x+2)}{2\sqrt{x^3+3x^2}}\)
\(y”=\displaystyle\frac{3}{2}\cdot\displaystyle\frac{(2x+2)\sqrt{x^3+3x^2}-(x^2+2x)\displaystyle\frac{3x^2+6x}{2\sqrt{x^3+3x^2}}}{x^3+3x^2}\)
\(=\displaystyle\frac{3}{4}\cdot\displaystyle\frac{x^3(x+4)}{(x^3+3x^2)^{\frac{3}{2}}}\)
よって増減表は次の通り。
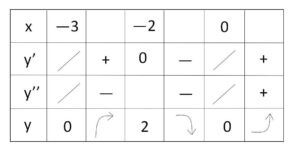
\(x\)軸対称に注意すると、曲線②の概形は次の通り。
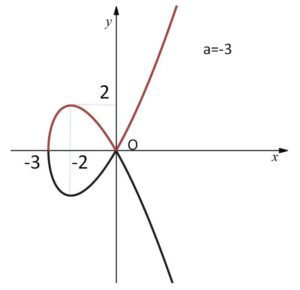
(3)
曲線 \(y^2=x^3-3x^2\)・・・③
\(y^2=x^2(x-3)\)
\(x^2(x-3)≧0\) より、定義域は \(x≧3\) または \(x=0\)
このとき③より
\(y=±\sqrt{x^3-3x^2}\)
\(y=\sqrt{x^3-3x^2}\) について
(ア)\(x=0\) のとき \(y=0\)
(イ)\(x>3\) のとき
\(y’=\displaystyle\frac{3x^2-6x}{2\sqrt{x^3-3x^2}}=\displaystyle\frac{3x(x-2)}{2\sqrt{x^3-3x^2}} \ (>0)\) より単調増加。
\(y”=\displaystyle\frac{3}{2}\cdot\displaystyle\frac{(2x-2)\sqrt{x^3-3x^2}-(x^2-2x)\cdot\displaystyle\frac{3x^2-6x}{2\sqrt{x^3-3x^2}}}{x^3-3x^2}\)
\(=\displaystyle\frac{3}{4}\cdot\displaystyle\frac{x^3(x-4)}{(x^3-3x^2)^{\frac{3}{2}}}\) (\(3<x<4\) で上に凸、\(x>4\) で下に凸)
したがって曲線③のグラフは次の通り。
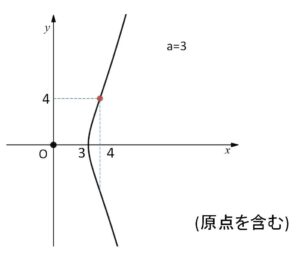
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→媒介変数表示とグラフの概形 back→グラフの増減と高次導関数