数値の大小を関数を用いて調べる例題です。
(例題1)
(1)\(x\)を正数とするとき、\(\log(1+\displaystyle\frac{1}{x})\) と \(\displaystyle\frac{1}{x+1}\) の大小を比較せよ。
(2)\((1+\displaystyle\frac{2001}{2002})^{\frac{2002}{2001}}\) と \((1+\displaystyle\frac{2002}{2001})^{\frac{2001}{2002}}\) の大小を比較せよ。
(解答)
(1)
\(f(x)=\log(1+\displaystyle\frac{1}{x})-\displaystyle\frac{1}{x+1}\) (\(x>0\)) とおくと
\(f'(x)=\displaystyle\frac{-\displaystyle\frac{1}{x^2}}{1+\displaystyle\frac{1}{x}}+\displaystyle\frac{1}{(x+1)^2}=-\displaystyle\frac{1}{x(x+1)}+\displaystyle\frac{1}{(x+1)^2}\)
\(=\displaystyle\frac{-1}{x(x+1)^2}\color{blue}{<0}\)
よって、\(f(x)\)は単調減少。
また、\(\displaystyle\lim_{x \to \infty}f(x)=0\) だから
\(f(x)>0\) が成り立つ。
したがって
\(\log(1+\displaystyle\frac{1}{x})>\displaystyle\frac{1}{x+1}\)
(2)
よって新たな関数を設定する必要がありますが、(2)の2つの数値に着目するとどちらも
\((1+\displaystyle\frac{1}{x})^{x}\) の形をしています。よってこの関数の増減を調べることになりますが、微分しやすいように対数をとって
\(g(x)=\log(1+\displaystyle\frac{1}{x})^{x}\)
の増減を考えます。これを微分すると(1)の2式が現れるのでしょう。
(\(g_1(x)=\log(1+x)^{\frac{1}{x}}\) とおく方法も考えられますが、(1)を踏まえて上の形にしておきます)
\(g(x)=\log(1+\displaystyle\frac{1}{x})^{x}\) (\(x>0\)) とおくと
\(g(x)=x\log(1+\displaystyle\frac{1}{x})\)
微分して
\(g'(x)=\log(1+\displaystyle\frac{1}{x})+x\cdot\displaystyle\frac{-\displaystyle\frac{1}{x^2}}{1+\displaystyle\frac{1}{x}}\)
\(=\log(1+\displaystyle\frac{1}{x})-\displaystyle\frac{1}{x+1}\)\(>0\) ((1)より)
よって \(g(x)\) は単調増加。
\(\displaystyle\frac{2001}{2002}<1<\displaystyle\frac{2002}{2001}\) より
\(g(\displaystyle\frac{2001}{2002})<g(\displaystyle\frac{2002}{2001})\)
\(\log(1+\displaystyle\frac{2002}{2001})^{\frac{2001}{2002}}<\log(1+\displaystyle\frac{2001}{2002})^{\frac{2002}{2001}}\)
底は \(e>1\) だから
\((1+\displaystyle\frac{2002}{2001})^{\frac{2001}{2002}}<(1+\displaystyle\frac{2001}{2002})^{\frac{2002}{2001}}\)
(例題2)
\(e^{π}\) と \(π^{e}\) の大小を比較せよ。
仮に \(e^{π}<π^{e}\) とすると、対数をって
\(π\log e<e\log π\)
さらに変形して
\(\displaystyle\frac{\log e}{e}<\displaystyle\frac{\log π}{π}\)
です。この流れは逆にもたどれるので、\(f(x)=\displaystyle\frac{\log x}{x}\) の増減を調べるとうまくいきそうです。
(解答)
\(f(x)=\displaystyle\frac{\log x}{x}\) (\(x>0\)) とおく。
\(f'(x)=\displaystyle\frac{\displaystyle\frac{1}{x}\cdot x-\log x\cdot1}{x^2}\)
\(=\displaystyle\frac{1-\log x}{x^2}\)
よって、
\(e≦x\) のとき \(f(x)\)は単調減少。
(\(0<x≦e\) のとき \(f(x)\)は単調増加)
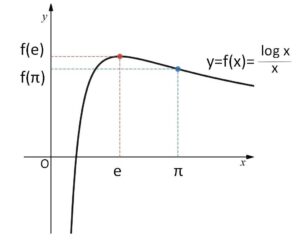
\(e<π\) (\(2.71<3.14\)) だから
\(f(e)>f(π)\)
ゆえに
\(\displaystyle\frac{\log e}{e}>\displaystyle\frac{\log π}{π}\)
\(π\log e>e\log π\)
\(\log e^{π}>\log π^{e}\)
対数の底\(e\)は\(1\)より大きいから
\(e^{π}>π^{e}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→軌跡・領域と微分 back→方程式の解と極限