2次以上の近似式

2次以上の近似式について見ていきます。

・2次以上の近似式
\(y=f(x)\) の \(x=a\) 付近での1次の近似式は

\(g_1(x)=f(a)+f'(a)(x-a)\)・・・(i)

であり、\(x=a\)における接線の方程式でした。そこで \(x=a\) で \(y=f(x)\) と接する2次式 \(y=g_2(x)\) を考えると、\(f(a)=g_2(a)\) より

\(g_2(x)=f(a)+(x-a)(px+q)\)・・・(ii)

おくとができます。ここで2次の近似式を考えたいので、もとの\(f(x)\)と1次、2次の微分係数が等しくなるようにすると(このとき接する)、\(g_2′(a)=f'(a)\)、\(g_2”(a)=f”(a)\) だから

\(g_2′(x)=(px+q)+(x-a)\cdot p\)
\(g_2”(x)=p+p\)

より
\(pa+q=f'(a)\)・・・①
\(2p=f”(a)\)・・・②

となるので、①②より
\(p=\displaystyle\frac{f”(a)}{2}\)、\(q=f'(a)-\displaystyle\frac{af”(a)}{2}\)
です。したがってこれらを(ii)に代入して整理すると

\(g_2(x)=f(a)+(x-a)\{\displaystyle\frac{f”(a)}{2}(x-a)+f'(a)\}\)

\(=f(a)+f'(a)(x-a)+\displaystyle\frac{f”(a)}{2}(x-a)^2\)・・・(ii)’

となります。ここで1次の近似式と(ii)’を比べると、2次式(ii)’では \(\displaystyle\frac{f”(a)}{2}(x-a)^2\) だけ加えられています。このことも考慮して\(f(x)\) と \(g_1(x),g_2(x)\) を同時にグラフで表すと次のようになりますが、どちらのほうが精度が高いかは \(\displaystyle\frac{f”(a)}{2}(x-a)^2\) の項の値によることになります。ただ、2次式のほうがより曲線的であることと、2回の微分係数(凹凸、傾きの増加率)まで等しいことから、2次式(ii)’のほうがよりもとの曲線に近いことが多いです。以上のことを踏まえて(ii)’を2次の近似式ということにします。

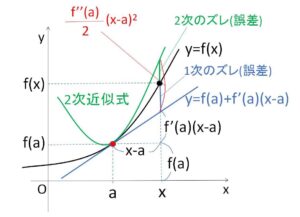
(微分係数は \(x \to a\) を考えるので、\(x\)が\(a\)に近いという条件を加えます)

(参考)
\(f(x)\) の \(x=a\) 付近の1次近似式、2次近似式は

\(g_1(x)=f(a)+f'(a)(x-a)\)
\(g_2(x)=f(a)+f'(a)(x-a)+\displaystyle\frac{f”(a)}{2}(x-a)^2\)

であり、
\(g_1(a)=f(a)\)、\(g_2′(a)=f'(a)\)
\(g_2(a)=f(a)\)、\(g_2′(a)=f'(a)\)、\(g_2”(a)=f”(a)\)
が成り立っています。

近似式の形と、微分係数の関係式から3次の近似式を
\(g_3(x)=p_0+p_1(x-a)+p_2(x-a)^2+p_3(x-a)^3\)
として、\(g_3(a)=f(a)\)、\(g_3′(a)=f'(a)\)、\(g_3”(a)=f”(a)\)、\(g_3”'(a)=f”'(a)\) が成り立つように\(p_0,p_1,p_2,p_3\)を決定すると

\(g_3(x)=f(a)+f'(a)(x-a)+\displaystyle\frac{f”(a)}{2}(x-a)^2+\displaystyle\frac{f”'(a)}{3!}(x-a)^3\)

です。同様に4次、5次・・・の近似式も考えていくと、\(n\)次の近似式は次のように表されることになります。

\(g_n(x)=\displaystyle\frac{f(a)}{0!}(x-a)^0+\displaystyle\frac{f'(a)}{1!}(x-a)+\displaystyle\frac{f”(a)}{2!}(x-a)^2+\cdots+\displaystyle\frac{f^{(n)}(a)}{n!}(x-a)^n\)

\(=\displaystyle\sum_{k=0}^{n}\displaystyle\frac{f^{(k)}(a)}{k!}(x-a)^k\)

さらに大まかにこの先の話をすると、近似式ではなくもとの関数\(f(x)\)と完全に一致させるために補正項(剰余項)を加えて(テーラーの定理)、 \(n \to \infty\) でこの剰余項が\(0\)に収束するとき、\(f(x)\)を上記\(g_n(x)\)の形の無限級数で表すことができる(テーラー展開)ということにつながっていきます。

(例題)
\(|x|\)が十分小さいとき、次の関数の1次近似式、2次近似式をそれぞれ求めよ。

(1)\(f(x)=e^x\)
(2)\(f(x)=\sin x\)
(3)\(f(x)=\cos x\)
(4)\(f(x)=\log(x+1)\)
(5)\(f(x)=\sqrt{x+1}\)

(解答)
(1)
\(f(x)=e^x\)、\(f'(x)=e^x\)、\(f”(x)=e^x\) より
\(f(0)=f'(0)=f”(0)=1\) だから

1次:\(f(x)≒1+x\)
2次:\(f(x)≒1+x+\displaystyle\frac{1}{2}x^2\)

(2)
\(f(x)=\sin x\)、\(f'(x)=\cos x\)、\(f”(x)=-\sin x\) より
\(f(0)=0\)、\(f'(0)=1\)、\(f”(0)=0\) だから

1次:\(f(x)≒x\)
2次:\(f(x)≒x\)

(3)
\(f(x)=\cos x\)、\(f'(x)=-\sin x\)、\(f”(x)=-\cos x\) より
\(f(0)=1\)、\(f'(0)=0\)、\(f”(0)=-1\) だから

1次:\(f(x)≒1\)
2次:\(f(x)≒1-\displaystyle\frac{1}{2}x^2\)

(4)
\(f(x)=\log(x+1)\)、\(f'(x)=\displaystyle\frac{1}{x+1}\)、\(f”(x)=-\displaystyle\frac{1}{(x+1)^2}\) より
\(f(0)=0\)、\(f'(0)=1\)、\(f”(0)=-1\) だから

1次:\(f(x)≒x\)
2次:\(f(x)≒x-\displaystyle\frac{1}{2}x^2\)

(5)
\(f(x)=(x+1)^{\frac{1}{2}}\)、\(f'(x)=\displaystyle\frac{1}{2}(x+1)^{-\frac{1}{2}}\)、\(f”(x)=-\displaystyle\frac{1}{4}(x+1)^{-\frac{3}{2}}\) より
\(f(0)=1\)、\(f'(0)=\displaystyle\frac{1}{2}\)、\(f”(0)=-\displaystyle\frac{1}{4}\) だから

1次:\(f(x)≒1+\displaystyle\frac{1}{2}x\)
2次:\(f(x)≒1+\displaystyle\frac{1}{2}x-\displaystyle\frac{1}{8}x^2\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→曲線の曲がり具合　back→微小変化量