外れ値について見ていきます。
・外れ値
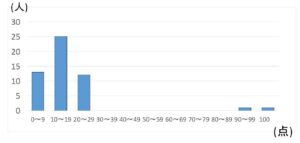
上のヒストグラムは、ある塾のクラスの\(100\)点満点のテスト結果です。
このグラフを見ると、グラフを主に特徴づけているのは\(0\)点から\(29\)点の範囲であり、\(90\)点以上の範囲は極端なデータになっています。
このように、他の値と比べて極端に大きい(小さい)値を外れ値といい、このテストの結果が、\(97\)点\(1\)人、\(100\)点\(1\)人とすると、\(97,100\)(点)が外れ値となります。
極端に大きい(小さい)というと曖昧な表現になってしまうので、どのような数値のときに外れ値になるかを定義する必要があり、それは次のようになります。(この外れ値の基準は厳格なもので無く、場合によっては変化しますが、よく利用される基準となっています)
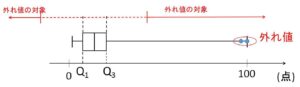
「第1四分位数-1.5×(四分位範囲) 以下の値」
「第3四分位数+1.5×(四分位範囲) 以上の値」
を外れ値とする。
第1四分位数と第3四分位数をそれぞれ\(Q_1,Q_3\)とすると、四分位範囲は\(Q_3-Q_1\)です。
よって、「\(Q_1-1.5(Q_3-Q_1)\) 以下」「\(Q_3+1.5(Q_3-Q_1)\) 以上」の値が外れ値です。
外れ値はデータの主な特徴を調べるときに邪魔な値になることが多く、特徴を調べるために外れ値を除いたりします。このテストの結果の例だと、ほとんどの生徒の点数が低いことからテストの難易度が高すぎると結論づけることになり、次回以降の難易度調整の目安になります。
しかし、外れ値が不必要なデータということではなく、外れ値が重要な意味を持っていることもよくある事です。このテストの結果でいうと2人の優秀な生徒が見つかったということになります。
・外れ値のデータの分析に関する影響
外れ値を分析に入れるか入れないかを考えると、データの分析において、次のような影響の大小があることが分かります。
(影響が大きいもの)
平均値、範囲(最大値・最小値)
外れ値は極端な値なので、平均値に大きな影響があります。また最大値や最小値にも当然大きく影響します。
(影響が小さいもの)
中央値、四分位範囲(四分位数)
外れ値は最小値・最大値付近のデータなので、四分位数関連の値は影響が小さいです。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。