仮説検定の手法について見ていきます。
・仮説検定
得られたデータから、ある仮説が正しいかどうかを判断する統計的手法を仮説検定(統計的仮説検定)と呼びます。次の具体例で検討してみます。
「\(A\)君と\(B\)君は、\(A\)君が用意したコインを使用してゲームを実施した。そのゲームはコインを\(10\)回投げて、表が多く出た場合は\(A\)君の勝ち、裏が多く出た場合は\(B\)君の勝ちという内容であった。そして表が\(9\)回出たので\(A\)君の勝ちになったが、\(B\)君はそのコインの表裏の出やすさについて疑問を抱いた。」
なんとなく\(A\)君が用意したコインは表が出やすそうと思えますが、これを論理的に判断する方法が仮説検定です。仮説検定ではまず示したい主張(仮説\(H_1\))を否定する仮説\(H_0\)を立てて、仮説\(H_0\)の妥当性を判断して間接的に\(H_1\)が正しいかどうか判断します。このとき、否定する仮説\(H_0\)を帰無仮説、主張したい仮説\(H_1\)を帰無仮説に対になっていることから対立仮説とよびます。この例だと次のようになります。
対立仮説\(H_1\):コインの表が裏より出やすい
帰無仮説\(H_0\):コインの表と裏は同じ確率で出る
さて帰無仮説ではコインの表と裏が等確率で出るので、そのもとで表が出る回数の各確率を求めると次のようになります。(反復試行の確率により求める)
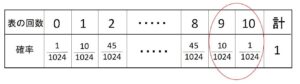
よって表が\(9\)回以上出る確率は(\(9\)回以上を考える理由は後述)
\(\displaystyle\frac{10+1}{1024}≒0.011\) (\(1.1%\))
となります。
すると、表と裏が等確率で出る場合には表が\(9\)回以上出る確率は約\(1.1%\)なので、このような稀な事は起きえないと判断することができます。しかし、\(1.1%\)くらいなら起きてもおかしくないと判断する人もいるでしょう。そこで判断基準を定めるために有意水準というものを考え、起きる確率がこの有意水準より大きいか小さいかで判断します。有意水準は通常 \(0.05\)(\(5%\)) か \(0.01\)(\(1%\)) を設定します。
例えば \(0.05\) だと \(5%\) より大きいことは起きえる(逆に\(5%\)以下のことは起きえない) と判断することになり、この例だと 「\(0.011<0.05\)」 より表と裏が同じ確率であることは妥当でない(帰無仮説は妥当でない)と判断されて、もとの仮説\(H_1\)が正しいと判断ができます。このとき帰無仮説\(H_0\)が妥当でないと判断することを、帰無仮説を棄却するといいます。
一方、有意水準が \(0.01\) の場合「\(0.011>0.01\)」より帰無仮説は棄却されません。このとき帰無仮説を積極採用するという意味では無く、設定したある帰無仮説ではおかしな点が見つからず(キズが見つからず)、もとの仮説\(H_1\)が正しいかどうかは分からないくらいのニュアンスであることに注意してください。この理由は数ⅡBの統計のところで少しだけ詳しく扱いますが、今の段階では背理法で矛盾が見つからなかった場合には、すぐさまもとの命題が間違っていると判断できないのと同じような理由と思ってください。
(まとめ)
帰無仮説\(H_0\)を棄却する→対立仮説\(H_1\)は正しいと判断
帰無仮説\(H_0\)を棄却しない→対立仮説\(H_1\)が正しいかどうか分からない
※\(9\)回以上と範囲でとる理由
\(9\)回単体の確率でなく、\(9\)回以上と範囲でとるのは数ⅡBで扱う仮説検定(範囲でとっている)と合わせるためです。またある\(1\)点だけの確率にしてしまうと、試行回数が多い場合には妥当な結論が得られません。例えばコインの例で試行回数を\(500\)回としてちょうど表と裏が\(250\)回ずつ出たとします。表裏が等確率で出る(帰無仮説)とすると、ちょうど表と裏が\(250\)回ずつ出る確率は約\(3.6%\)。これを有意水準\(5%\)で検定すると、帰無仮説が棄却されて表裏が等確率でない(対立仮説が正しい)と判断することになってしまいます(この結論は変)。
・仮説検定の過誤
有意水準\(5%\)で検定をするとき、\(5%\)以下の確率で起きることは稀なケースであると判断をしますが、逆に言うと帰無仮説が正しい場合であっても\(5%\)以下の確率で起きえてしまう事です。そこでこの有意水準は帰無仮説が正しい場合であっても間違って棄却されてしまう確率を表していることから危険率とも呼ばれます。またこの「帰無仮説が正しい場合に間違って棄却してしまう」ことを第一種の過誤といいます。
一方、「帰無仮説が間違っている場合に棄却しない」過誤もあり、これを第二種の過誤といいます。
第一種の過誤の確率を減らすには有意水準を下げればよいですが、下げれば下げるほど帰無仮説が棄却されにくくなるので第二種の過誤の確率が増えることになります。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。