前回と同じ例を用いて、代表値について学んでいきます。
(例)
A先生のクラスの生徒は16人である。このクラスの生徒が数学のテストを受験したとき、その結果を\(x_i\)とすると \((i=1,2・・・16)\) 次のようになった。
\(x_1=62,x_2=76,x_3=42,x_4=55\)
\(x_5=96,x_6=88,x_7=35,x_8=63\)
\(x_9=82,x_{10}=48,x_{11}=51,x_{12}=58\)
\(x_{13}=61,x_{14}=84,x_{15}=69,x_{16}=76\)
\(x_1=62,x_2=76,x_3=42,x_4=55\)
\(x_5=96,x_6=88,x_7=35,x_8=63\)
\(x_9=82,x_{10}=48,x_{11}=51,x_{12}=58\)
\(x_{13}=61,x_{14}=84,x_{15}=69,x_{16}=76\)
この例は想像上でのお話ですが、実際に自分がテストを受けてみてほとんどの人が気になるのはテストの平均点で、自分の点数と全体の出来を比べたいわけですね。テストの平均点は全体の出来の指標であり、平均値(テストの平均点)のようにデータ全体の特性を適当な数値で表したものを代表値といいます。代表値には平均値のほかに、中央値、最頻値がよく用いられます。
・平均値
大きさ\(n\)のデータの値を\(x_1,x_2・・・x_{n}\)とすると、各値の総和を\(n\)で割ったものを平均値といいます。
大きさ\(n\)のデータの値を\(x_1,x_2・・・x_{n}\)とすると、各値の総和を\(n\)で割ったものを平均値といいます。
\(\bar{x}=\displaystyle\frac{x_1+x_2+・・・+x_{n}}{n}\)
他の代表値もそうですが、平均値はあくまでもデータの特徴の目安です。例えば、10人のクラスがいてテストを受けたとしましょう。10人全員が10点を取った場合平均点(平均値)は10点です。また、1人が100点を取って9人が0点を取った場合でも平均点(平均値)は10点です。この2通りのデータは明らかに同じではないですね。平均点だけでデータ全てを特徴づけるわけではありません。
例の平均値を計算すると
\(\bar{x}=\displaystyle\frac{x_1+x_2+・・・+x_{16}}{16}=\displaystyle\frac{1046}{16}≒65.4\)
\(\bar{x}=\displaystyle\frac{x_1+x_2+・・・+x_{16}}{16}=\displaystyle\frac{1046}{16}≒65.4\)
となります。
・中央値(メジアン)
データの値を大きさの順に並べたときに、中央にくる値のことを中央値(メジアン)といいます。中央値はデータの値の個数が、奇数のときは中央の値になりますが、偶数の場合にはちょうど中央の値が存在しないため、中央にある2つの値の平均値とします。
データの値を大きさの順に並べたときに、中央にくる値のことを中央値(メジアン)といいます。中央値はデータの値の個数が、奇数のときは中央の値になりますが、偶数の場合にはちょうど中央の値が存在しないため、中央にある2つの値の平均値とします。
例ではデータの値の個数が16個で偶数なので、中央にある2つの値を探します。実際に並べると、
\(y_1=35,y_2=42,y_3=48,y_4=51\)
\(y_5=55,y_6=58,y_7=61,y_8=62\)
\(y_9=63,y_{10}=69,y_{11}=76,y_{12}=76\)
\(y_{13}=82,y_{14}=84,y_{15}=88,y_{16}=96\)
\(y_5=55,y_6=58,y_7=61,y_8=62\)
\(y_9=63,y_{10}=69,y_{11}=76,y_{12}=76\)
\(y_{13}=82,y_{14}=84,y_{15}=88,y_{16}=96\)
となり、中央の2つの値は、\(y_8=62,y_9=63\)なので、
(中央値)\(=m_{e}=\displaystyle\frac{62+63}{2}=62.5\)
(中央値)\(=m_{e}=\displaystyle\frac{62+63}{2}=62.5\)
中央値はざっくりとですがデータの分布の偏りがわかります。
・最頻値(モード)
最も度数のデータの値を最頻(さいひん)値(モード)といいます。例では \(y_{11}=y_{12}=76\)なので (最頻値)=\(m_{o}=76\) となります。
最も度数のデータの値を最頻(さいひん)値(モード)といいます。例では \(y_{11}=y_{12}=76\)なので (最頻値)=\(m_{o}=76\) となります。
また、度数分布表でデータが整理されているときは、最も度数が大きい階級の階級値となります。
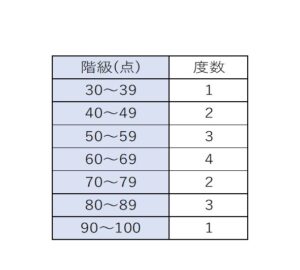
最も度数が大きい階級は 60~69なので、度数分布表での最頻値は \(\displaystyle\frac{60+69}{2}=64.5\)となります。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。