データの散らばりに関する量やグラフについて学んでいきます。
これから学ぶ事項はデータの散らばりに関するものです。散らばりとはデータの値が集中しているのか、離れているのかを表すものです。散らばりが大きいときは値がばらばらに離れている傾向があるということです。
・範囲
データの値の最大値と最小値の差を範囲といいます。
テストの点数でいうと、最高点と最低点の差です。範囲の値が大きいと散らばりが大きいことになります。
・四分位数
データの値を小さい順に並べたときデータを4等分する位置の値を四分位数(しぶんいすう)といいます。仕切りが3つあれば4等分されるので四分位数は全部で3つあります。
小さい方から順に、第1四分位数(\(Q_1)\)、第2四分位数(\(Q_2)\)、第3四分位数(\(Q_3)\)とよびます。第2四分位数(\(Q_2)\)は中央値となります。
データの値を小さい順に並べたときデータを4等分する位置の値を四分位数(しぶんいすう)といいます。仕切りが3つあれば4等分されるので四分位数は全部で3つあります。
小さい方から順に、第1四分位数(\(Q_1)\)、第2四分位数(\(Q_2)\)、第3四分位数(\(Q_3)\)とよびます。第2四分位数(\(Q_2)\)は中央値となります。
4等分する値なので、中央値を求める要領を繰り返すことで四分位数を求めることができます。まずデータの値を小さい順にならべ、真ん中の値(中央値=第2四分位数)を求めます。そこを基準として下半分と上半分のデータに分けます。下半分と上半分の中央値がそれぞれ第1四分位数、第3四分位数となります。
(例)

(例)

・四分位範囲・四分位偏差
第3四分位数から第1四分位数を引いた\(Q_3-Q_1\)を四分位範囲、四分位範囲を2で割った \(\displaystyle\frac{Q_3-Q_1}{2}\)を四分位偏差といいます。
第3四分位数から第1四分位数を引いた\(Q_3-Q_1\)を四分位範囲、四分位範囲を2で割った \(\displaystyle\frac{Q_3-Q_1}{2}\)を四分位偏差といいます。
四分位範囲は中半分(全体の\(\displaystyle\frac{1}{4}\)の2倍)の範囲です。上の例では\(Q_3-Q_1=5\)です。四分位範囲が大きいと中半分の散らばりが大きいことになります。四分位偏差は四分位範囲の半分の大きさですが、必ずしも第3四分位数から第2四分位数(中央値)を引いた\(Q_3-Q_2\)とはなりません。
・箱ひげ図
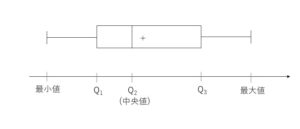
最大値・最小値・四分位数(計5つ)をグラフで視覚化したものを箱ひげ図といいます。平均値も書き込むときは+で記入します。
最大値・最小値・四分位数(計5つ)をグラフで視覚化したものを箱ひげ図といいます。平均値も書き込むときは+で記入します。
(例題)
次の表はあるクラス45人に10点満点のテストを行った結果である。
次の表はあるクラス45人に10点満点のテストを行った結果である。

(1)データの範囲と四分位数を求めよ。
(2)四分位範囲と四分位偏差を求めよ。
(3)箱ひげ図をかけ。
(2)四分位範囲と四分位偏差を求めよ。
(3)箱ひげ図をかけ。
(解答)
(1)
(1)
データの範囲は\(10-2=\)\(8\)(点)
四分位数については45人のデータの値を並べるのは大変なので四分位数がどの位置にあるのかを調べます。45は奇数なので中央値は小さい順に並べて23番目の値です。下半分は22個データの数があるので11番目と12番目の値の平均値が\(Q_1\)、上半分22個については34番目と35番目の値の平均値が\(Q_3\)となります。
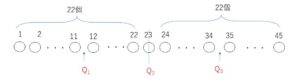

第2四分位数\(Q_2\)は小さい順に並べて23番目の値。
よって\(Q_2=6\)(点)
よって\(Q_2=6\)(点)
第1四分位数\(Q_1\)は11番目の値\(5\)と12番目の値\(5\)の平均値となり
\(Q_1=5\)(点)
\(Q_1=5\)(点)
第3四分位数\(Q_3\)は34番目の値\(7\)と35番目の値\(7\)の平均値であり
\(Q_3=7\)(点)
\(Q_3=7\)(点)
(2)
(四分位範囲)\(=Q_3-Q_1=7-5=\)\(2\)(点)
(四分位範囲)\(=Q_3-Q_1=7-5=\)\(2\)(点)
(四分位偏差)\(=\displaystyle\frac{2}{2}=\)\(1\)(点)
(3)
箱ひげ図は以下の通り。
箱ひげ図は以下の通り。
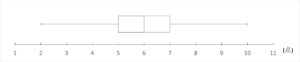
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。