分散と標準偏差 | 教えて数学理科

平均値からの散らばりの大きさについての指標について学んでいきます。

・分散
\(n\)個のデータの値 \(x_1,x_2・・・,x_{n}\) の平均値を\(\bar{x}\)としたとき、\(x_1-\bar{x},x_2-\bar{x},・・・,x_{n}-\bar{x}\)をそれぞれ、\(x_1,x_2・・・,x_{n}\)の平均値からの偏差といいます。そして偏差の2乗の平均を分散といいます。つまり分散\(s^2\)は

\(s^2=\displaystyle\frac{1}{n}\{(x_1-\bar{x})^2+(x_2-\bar{x})^2+・・・+(x_{n}-\bar{x})^2\}\)・・・①

と表されます。

分散は平均値からのデータの散らばり方を表す数値です。大きいほど散らばりが大きくなります。2乗しているのは、偏差のままの平均だと平均値より大きい値と小さい値の場合の偏差が＋と－になり打ち消しあうからです。

また、①を変形することで

\(s^2=\bar{x^2}-(\bar{x})^2\)・・・②

が導かれます。

\(\bar{x^2}\)は\(x^2\)の平均値で、\((\bar{x})^2\)は\(x\)の平均値の2乗です。全く違うものです。証明を見ると分かりやすいと思います。

(②の証明)
2乗の式を展開して整理していくと

\(s^2=\displaystyle\frac{1}{n}\{(x_1-\bar{x})^2+(x_2-\bar{x})^2+・・・+(x_{n}-\bar{x})^2\}\)

\(=\displaystyle\frac{1}{n}\{(x_1^2+x_2^2+・・・+x_{n}^2)\)
\(-2\bar{x}(x_1+x_2+・・・+x_{n})+n(\bar{x})^2\}\)

\(=\displaystyle\frac{1}{n}(x_1^2+x_2^2+・・・+x_{n}^2)\)
\(-2\bar{x}・\displaystyle\frac{1}{n}(x_1+x_2+・・・+x_{n})+(\bar{x})^2\)

\(=\bar{x^2}-2\bar{x}・\bar{x}+(\bar{x})^2\)

\(=\bar{x^2}-(\bar{x})^2\)

・標準偏差
分散の正の平方根を標準偏差といいます。つまり標準偏差\(s\)は

\(s=\sqrt{\displaystyle\frac{1}{n}\{(x_1-\bar{x})^2+(x_2-\bar{x})^2+・・・+(x_{n}-\bar{x})^2\}}\)

\(=\sqrt{\bar{x^2}-(\bar{x})^2}\)

となります。

偏差を2乗すると単位も2乗されるため、もとのデータの単位とあわせるため平方根をとります。大きさも平方根をとることで、もとのデータのスケールに合わせています。

では実際に分散と標準偏差を求めてみます。

(例題)
ダーツを投げるゲームをして次の10個の得点を得た。

\(7,3,6,8,3,9,9,8,8,4\)

このデータの分散と標準偏差を小数第2位まで求めよ。

(解答)

分散を求めるために平均値をまず求めます。分散が求まれば標準偏差は平方根をとるだけです。

各得点\(x\)と\(x^2\)とそれぞれの総和は次の表のとおり。

よって平均値\(\bar{x}\)は
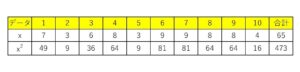
\(\bar{x}=\displaystyle\frac{65}{10}\)

分散\(s^2\)は
\(s^2=\bar{x^2}-(\bar{x})^2=\displaystyle\frac{473}{10}-(\displaystyle\frac{65}{10})^2=\)\(5.05\)

標準偏差\(s\)は
\(s=\sqrt{5.05}≒\)\(2.25\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。

→高校数学TOP　next→2つのデータ合計の分析　　 back→箱ひげ図の読み取り