もとのデータの変量\(x\)に対して、\(y=ax+b\) (\(a,b\)は定数)と新たな変量\(y\)を定義したとき、\(y\)の平均値や分散は\(x\)の平均値と分散とどのような関係があるのでしょうか。
・変量の変換(平均値)
もとの変量\(x\)のデータ(個数\(n\))の値を、\(x_1,x_2,・・・x_{n}\)として、あらたな変量\(y\)を \(y=ax+b\) と定義し、\(y_{i}=ax_{i}+b\) (\(i=1,2,・・・n)\)とします。\(x\)の平均値を\(\bar{x}\)、\(y\)の平均値を\(\bar{y}\)とすると、
\(\bar{y}=\displaystyle\frac{1}{n}(y_1+y_2+・・・+y_{n})\)
\(=\displaystyle\frac{1}{n}\{(ax_1+b)+(ax_2+b)+・・・+(ax_{n}+b)\}\)
\(=a・\displaystyle\frac{1}{n}(x_1+x_2+・・・+x_{n})+\displaystyle\frac{1}{n}・(nb)\)
\(=a\bar{x}+b\)
\(\bar{y}=a\bar{x}+b\)
さきほどと同様に\(y\)を定義します。\(x\)の分散を\(s_{x}^2\)、\(y\)の分散を\(s_{y}^2\)とすると、\(\bar{y}=a\bar{x}+b\)より
\(s_{y}^2=\displaystyle\frac{1}{n}\{(y_1-\bar{y})^2+(y_2-\bar{y})^2+・・・+(y_{n}-\bar{y})^2\}\) (分散の定義)
\(=\displaystyle\frac{1}{n}[\{(ax_1+b)-(a\bar{x}+b)\}^2+\)
\(\{(ax_2+b)-(a\bar{x}+b)\}^2+・・・\)
\(+\{(ax_{n}+b)-(a\bar{x}+b)\}^2]\)
\(=\displaystyle\frac{1}{n}\{a^2(x_1-\bar{x})^2+a^2(x_2-\bar{x})^2+・・・\)
\(+a^2(x_{n}-\bar{x})^2\}\)
\(=a^2\displaystyle\frac{1}{n}\{(x_1-\bar{x})^2+(x_2-\bar{x})^2+・・・+(x_{n}-\bar{x})^2\}\)
\(=a^2s_{x}^2\)
\(s_{y}^2=a^2s_{x}^2\)
\(s_{y}=\sqrt{a^2s_{x}^2}=|a|s_{x}\)
\(s_{y}=|a|s_{x}\)
(例題1)
変量\(x\)のデータの平均値を\(\bar{x}=\displaystyle\frac{37}{10}\)、分散を\(s_{x}^2=\displaystyle\frac{201}{100}\) とする。
(1)\(y=10(x-3)\)と定義された変量\(y\)の平均値と分散と標準偏差を求めよ。
(2)\(x\)の標準偏差を\(s_x\)とするとき、\(z=\displaystyle\frac{x-\bar{x}}{s_x}\)で定義された変量\(z\)の平均値と分散を求めよ。
(解答)
(1)求める平均値、分散、標準偏差を\(\bar{y},s_{y}^2,s_{y}\)とすると
\(y=10x-30\)だから
\(\bar{y}=10\bar{x}-30=10・\displaystyle\frac{37}{10}-30=\)\(7\)
\(s_{y}^2=10^2s_{x}^2=100・\displaystyle\frac{201}{100}=\)\(201\)
\(s_{y}=|10|s_{x}=10・\sqrt{\displaystyle\frac{201}{100}}=\)\(\sqrt{201}\)
(2)
求める平均値、分散を\(\bar{z},s_{z}^2\)とすると
\(\bar{z}=\displaystyle\frac{\bar{x}-\bar{x}}{s_x}=\)\(0\)
\(s_{z}^2=\displaystyle\frac{1}{s_x^2}s_x^2=\)\(1\)
次の変量\(x\)のデータについて以下の問いに答えよ。
(1)\(x\)と\(y\)の値を表にすると次の通り。

\(\bar{y}=\bar{x}-60\)だから、
\(\bar{x}=\bar{y}+60=2.5+60=\)\(62.5\)
\(\bar{x}=x_0+\bar{y}\)
\(=x_0+\displaystyle\frac{1}{n}\{(x_1-x_0)+(x_2-x_0)+・・・(x_{n}-x_0)\}\)
となるので、見積もった平均にずれの平均値を足してやることで真の平均値を求めることができます。
\(s_{u}^2=\bar{u^2}-(\bar{u})^2\) なので、\(u\)と\(u^2\)の平均値を計算します。
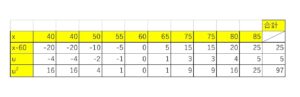
\(\bar{u}=\displaystyle\frac{5}{10}\)
\(s_{u}^2=\bar{u^2}-(\bar{u})^2=\displaystyle\frac{97}{10}-(\displaystyle\frac{5}{10})^2=\displaystyle\frac{945}{100}\)であり
\(s_{u}=\sqrt{\displaystyle\frac{945}{100}}=\displaystyle\frac{3\sqrt{105}}{10}\)
\(s_{x}=|5|s_{u}=5・\displaystyle\frac{3\sqrt{105}}{10}=\)\(\displaystyle\frac{3\sqrt{105}}{2}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。