複素数平面と平行移動

複素数平面の定義と、複素数の実数倍、和・差と複素数平面の関係について見ていきます。

・複素数平面

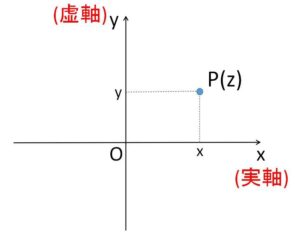
実数は数直線によって平面上の点として表すことができましたが、複素数も同様に平面上の点として図示することを考えます。複素数\(z\)は実数\(x,y\)を用いて

\(z=x+yi\)

で表されますが、これを通常の座標平面上の点 \((x,y)\) に対応させます。
すると、すべての複素数はそれぞれ平面上の1つの点で表され、また平面上のすべての点はそれぞれ1つの複素数で表されます。
このように、複素数\(x+yi\)を平面上の点\(P(x,y)\)で表す場合、この平面を複素数平面(複素平面、ガウス平面)とよびます。複素数平面では\(x,y\)軸はそれぞれ、実軸・虚軸とよばれ、実軸上の点は \(y=0\) より実数を表し、虚軸上の点は原点を除くと \(x=0,y≠0\) より純虚数(\(2i,-3i\)のような実数部分がない虚数)を表します。
また \(z=x+yi\) を表す点\(P\)を単に点\(z\)とよび、\(P(z)\)や\(P(x+yi)\)のように表します。

複素数を平面上の点として表すことにより、和や積などの複素数の演算を平面上の動きに対応させることで図形的処理が可能になります。

・複素数の実数倍、和・差と複素数平面
(実数倍)
\(0\)でない複素数 \(z=a+bi\) (\(a,b\)は実数) について、\(k\)を実数とすると

\(w=kz=ka+kbi\)・・・①

の表す点\(Q(w)\)は、原点と\(z\)を表す点を\(O(0),P(z)\)とおくと、①の形から直線\(OP\)上にあり、\(OQ=|k|OP\)を満たす点になります。絶対値を用いたのは\(k\)が正負の場合があるからで

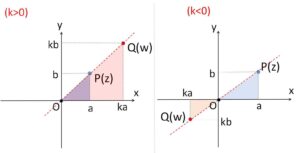
(i)\(k>0\) のとき
\(Q\)は\(O\)に関して\(P\)と同じ側にあり、\(OQ\)の長さは\(OP\)の\(k\)倍。

(ii)\(k=0\) のとき
\(Q\)は\(O\)と一致。

(iii)\(k<0\) のとき
\(Q\)は\(O\)に関して\(P\)と反対側にあり、\(OQ\)の長さは\(OP\)の\(|k|\)倍。

また、逆に\(O,P,Q\)が1直線上にあるとき \(w=kz\) と表されるので次のことが成り立ちます。
\(z≠0\) のとき
「3点\(0,z,w\)が一直線上にある \(⇔\) \(w=kz\) (\(k\)は実数)」

(和・差)
複素数の和・差は、実部・虚部ずつで計算し、それは虚数平面上で\(x,y\)成分それぞれの和・差となるのでベクトルの和・差と同様の内容になります。

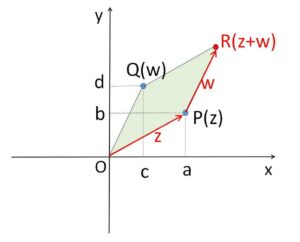
つまり
\(z=a+bi\)、\(w=c+di\)
とおくと

\(z+w=(a+c)+(b+d)i\)

なので、点\(R(z+w\))は点\(P(z)\)を「実軸方向に\(c\)、虚軸方向に\(d\)だけ平行移動した点」となります。これは\(Q(w)\)とおくと、ベクトルの和
\(\overrightarrow{OR}=\overrightarrow{OP}+\overrightarrow{OQ}\ (=\overrightarrow{OP}+\overrightarrow{PR})\)
に対応します。すると、複素数の和をベクトルのように位置を気にしないで捉えることができるので、\(O \to P \to R\) の移動を便宜上
\(\overrightarrow{OP}+\overrightarrow{PR}=z+w\)
と書くことも可能となります。

同様に差についても

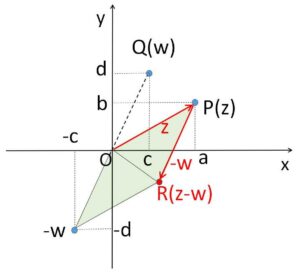
\(z-w=(a-c)+(b-d)i\)

なので、点\(R(z-w\))は点\(P(z)\)を「実軸方向に\(-c\)、虚軸方向に\(-d\)だけ平行移動した点」となり、
\(\overrightarrow{OP}+\overrightarrow{PR}=z-w\)
と表すことが可能です。

(例題)
\(α=2+2i\)、\(β=3-2i\)、\(γ=-1-i\)、\(δ\)を複素数として、複素数平面上に \(A(α),B(β),C(γ),D(δ)\) がある。四角形\(ABCD\)が平行四辺形になるとき、\(δ\)を求めよ。

(解答)

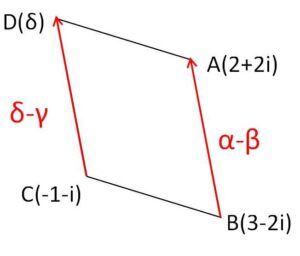
\(\overrightarrow{BA}=\overrightarrow{CD}\) より
\(δ-γ=α-β\)
よって
\(δ=γ+α-β\)
\(=(-1-i)+(2+2i)-(3-2i)\)
\(=-2+3i\)

(別解)

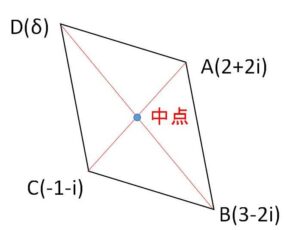
\(AC\)と\(BD\)の中点は一致するので
\(\displaystyle\frac{α+γ}{2}=\displaystyle\frac{β+δ}{2}\)
よって
\(δ=α+γ-β\)
\(=-2+3i\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→複素数平面と共役複素数