対称移動と複素数

複素数を利用した対称移動(線対称移動)について見ていきます。

・直線に対する対称移動(複素数)
共役複素数をとると、複素数平面上では実軸対称移動をすることを利用して「回転と共役複素数」を組み合わせることで、ある直線に関する対称移動を考えることができます。

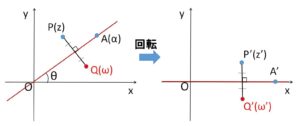
まずは原点を通る直線に関する対称移動です。
原点\(O\)と\(A(α)\) (\(α≠0\)) を通る直線を\(l\)とし、\(l\)について点\(P(z)\)と対称な点\(Q(ω)\)を表す複素数\(ω\)を求めてみます。

直線\(OA\)が実軸に重なるように全体を\(OA\)と実軸のなす角\(θ\)だけ時計回りに回転させ、移動後の2点を\(P'(z’),Q'(ω’)\)とします。
回転は複素数では積や商で表現できますが、\(α\)の絶対値は\(1\)とは限らないので、そのまま\(α\)で掛けたり割ったりすると拡大縮小までしてしまいます。そこで、\(\displaystyle\frac{α}{|α|}\) として大きさで割ることで回転だけ処理できるようにします(ベクトルでいう単位ベクトルのようなもの)。

時計回りの回転なので\(\displaystyle\frac{α}{|α|}\)との商を考えて
\(ω’=\displaystyle\frac{ω}{\displaystyle\frac{α}{|α|}}\)、\(z’=\displaystyle\frac{z}{\displaystyle\frac{α}{|α|}}\)

点\(z’\)と\(ω’\)は実軸対称になるので
\(ω’=\bar{z’}\)

したがって
\(\displaystyle\frac{ω}{α}|α|=\overline{\displaystyle\frac{z}{α}|α|}\)
より、\(|α|=\overline{|α|}\) (\(|α|\)は実数なので共役複素数をとっても同じ) だから

\(ω=\displaystyle\frac{α}{\overline{α}}\bar{z}\)
(分母分子\(α\)倍すると \(ω=\displaystyle\frac{α^2}{|α|^2}\bar{z}\))

となります。

もしくは次のように考えてもよいです。
「\(-θ\)回転→実軸対称移動→\(θ\)回転(元に戻す)」
の組み合わせを考えることで
\(\displaystyle\frac{z}{α}|α| \to \displaystyle\frac{\bar{z}}{\bar{α}}|α| \to \displaystyle\frac{\bar{z}}{\bar{α}}|α|×\displaystyle\frac{α}{|α|}\)
より
\(ω=\displaystyle\frac{α}{\overline{α}}\bar{z}\)

直線が原点を通らない場合は、最初に直線が原点を通るように平行移動させれば上記の方法に帰着できます。

(例題)
原点を\(O\)とする複素数平面上に、\(O\)と異なる点\(A(α)\)、および、2点\(O,A\)を通る直線\(l\)があるとき、以下の問いに答えよ。ただし必要ならば、直線\(l\)に関して\(P(z)\)と対称な点を\(P'(z’)\)とするとき、\(z’=\displaystyle\frac{α}{\bar{α}}\bar{z}\) が成り立つことを利用してよい。

(1)\(α=3+i\) とし、\(β=2+4i\) を表す点を\(B\)とおく。点\(B\)の直線\(l\)に関して対称な点を\(B'(β’)\)とするとき、\(β’\)を求めよ。
(2)さらに \(γ=-8+7i\) を表す点を\(C\)とする。線分\(OA\)上の点\(Q(ω)\)について、\(\angle AQB=\angle CQO\) が成り立つときの\(ω\)を求めよ。

(解答)
(1)
\(β’=\displaystyle\frac{α}{\bar{α}}\bar{β}\)

\(=\displaystyle\frac{3+i}{3-i}(2-4i)\)

\(=\displaystyle\frac{(10-10i)(3+i)}{10}\)

\(=(1-i)(3+i)\)

\(=4-2i\)

(2)

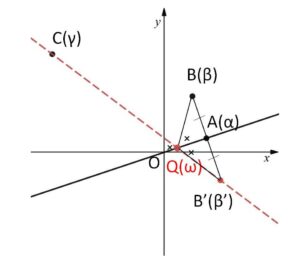
\(\angle AQB’=\angle AQB=\angle CQO\) だから
\(C,Q,B’\)は一直線上にある。

\(Q(ω)\)は直線\(CB’\)上にあることから\(k\)を実数とすると
\(ω=γ+k(β’-γ)\)
\(=(-8+7i)+k(4-2i+8-7i)\)
\(=(12k-8)+(-9k+7)i\)・・・①

\(Q(ω)\)は線分\(OA\)上にもあるので\(t\)を実数とすると
\(ω=t(3+i)\)
\(=3t+ti\)・・・②

\(k,t\)は実数だから①②より実部と虚部を比較して
\(12k-8=3t\)・・・③
\(-9k+7=t\)・・・④

③④より
\(k=\displaystyle\frac{29}{39}\)、\(t=\displaystyle\frac{4}{13}\)

\(0<t<1\) より、\(Q\)は線分\(OA\)上にある。よって②より
\(ω=\displaystyle\frac{12}{13}+\displaystyle\frac{4}{13}i\)

(注)
\(A\)はちょうど\(BB’\)の中点になっていますが、これはたまたまです。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→角の2等分線と複素数　back→内心・外心と複素数