複素数を用いた角の2等分線の方向の表し方です。
・角の2等分線の方向を表す複素数
複素数平面上に1直線上にない3点\(A(α),B(β),C(γ)\)があり、\(\angle ABC\)の2等分線を考えます。
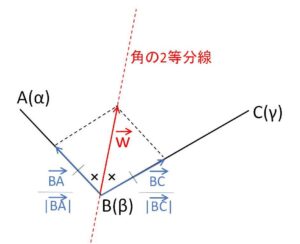
ベクトルを用いると \(\angle ABC\) の2等分線の方向ベクトルの向きは、2つの単位ベクトル \(\displaystyle\frac{\overrightarrow{BA}}{|\overrightarrow{BA}|},\ \displaystyle\frac{\overrightarrow{BC}}{|\overrightarrow{BC}|}\) で作られる平行四辺形(ひし形)の対角線の方向となるので、角の2等分線の方向ベクトル\(\vec{w}\)の1つは
\(\vec{w}=\displaystyle\frac{\overrightarrow{BA}}{|\overrightarrow{BA}|}+ \displaystyle\frac{\overrightarrow{BC}}{|\overrightarrow{BC}|}\)
これを複素数に対応させると、角の2等分線の方向を表す複素数\(ω\)の1つは次のようになることが分かります。
\(ω=\displaystyle\frac{α-β}{|α-β|}+\displaystyle\frac{γ-β}{|γ-β|}\)
(例題)
複素数平面上で、3点 \(1+2i\)、\(2+i\)、\(4+2i\) を順に\(A,B,C\)とする。\(B\)を通る直線\(l\)があって、\(B\)を通り\(l\)に垂直な直線\(n\)は、\(\angle ABC\) を2等分している。
(1)直線\(n\)の方向を表す複素数を1つ求めよ。
(2)直線\(l\)の方向を表す複素数を1つ求めよ。
(3)直線\(l\)と実軸との交点を求めよ。
(解答)
(1)
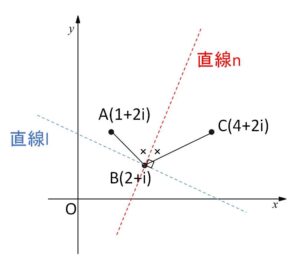
求める複素数を\(ω_1\)とすると
\(ω_1=\displaystyle\frac{(1+2i)-(2+i)}{|(1+2i)-(2+i)|}+\displaystyle\frac{(4+2i)-(2+i)}{|(4+2i)-(2+i)|}\)
\(=\displaystyle\frac{-1+i}{|-1+i|}+\displaystyle\frac{2+i}{|2+i|}\)
\(=\displaystyle\frac{-1+i}{\sqrt{2}}+\displaystyle\frac{2+i}{\sqrt{5}}\)
(2)
直線\(l,n\)は直交するので、\(l\)の方向を表す複素数を\(ω_2\)とすると
\(ω_2=iω_1\)
\(=\displaystyle\frac{-1-i}{\sqrt{2}}+\displaystyle\frac{-1+2i}{\sqrt{5}}\)
(3)
(共役複素数を利用した直線の方程式を利用する場合は、最後に実数条件 \(\bar{z}=z\) を使えばよい)
\(\sqrt{10}ω_2\)も\(l\)の方向を表す複素数であり
\(\sqrt{10}ω_2\)\(=\sqrt{5}(-1-i)+\sqrt{2}(-1+2i)\)
\(=-(\sqrt{2}+\sqrt{5})+(2\sqrt{2}-\sqrt{5})i\)
だから、直線\(l\)上にある複素数\(z\)は次のように表される。(\(k\)は実数)
\(z=(2+i)+k\{-(\sqrt{2}+\sqrt{5})+(2\sqrt{2}-\sqrt{5})i\}\)
\(=2-k(\sqrt{2}+\sqrt{5})+\{1+k(2\sqrt{2}-\sqrt{5})\}i\)・・・①
\(l\)と実軸の交点を表す複素数は実数だから、①より
\(1+k(2\sqrt{2}-\sqrt{5})=0\)
よって
\(k=\displaystyle\frac{-1}{2\sqrt{2}-\sqrt{5}}\)
したがって交点を表す複素数は①より
\(z=2+\displaystyle\frac{\sqrt{2}+\sqrt{5}}{2\sqrt{2}-\sqrt{5}}\)
\(=2+\displaystyle\frac{(\sqrt{2}+\sqrt{5})(2\sqrt{2}+\sqrt{5})}{3}\)
\(=2+\displaystyle\frac{9+3\sqrt{10}}{3}\)
\(=5+\sqrt{10}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→図形と複素数の対応関係 back→対称移動と複素数