複素数の問題を図形的に処理する例題です。
(例題1)
複素数\(α,β\)が
\(|α|=|β|=|α-β|=1\)
を満たしている。
(1)\(|2β-α|\) の値を求めよ。
(2)\(\displaystyle\frac{β}{α}\) の値を求めよ。
(1)
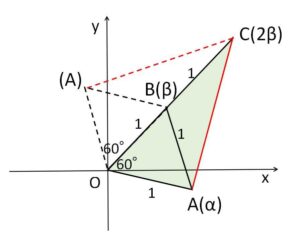
複素数平面上において\(A(α),B(β)\)とおくと
\(OA=OB=AB=1\)
だから、\(△OAB\)は1辺の長さが\(1\)の正三角形。
\(C(2β)\)とおくと、\(C\)は\(OB\)の延長線にあり、\(OC=2\)。
\(|2β-α|\)は\(AC\)の長さだから、\(△OCA\)において余弦定理より
\(AC^2=OA^2+OC^2-2OA \cdot OC\cos\displaystyle\frac{π}{3}\)
\(=1+4-2\)
\(=3\)
より
\(|2β-α|=\sqrt{3}\)
(2)
(1)の図より
\(\displaystyle\frac{β}{α}=\cos(±\displaystyle\frac{π}{3})+i\sin(±\displaystyle\frac{π}{3})\)
\(=\displaystyle\frac{1±\sqrt{3}i}{2}\)
(別解)
(1)
\(|α|=|β|=|α-β|=1\)
\(|α-β|^2=1\) より
\(|α|^2-(α\bar{β}+\bar{α}β)+|β|^2=1\)
\(1-(α\bar{β}+\bar{α}β)+1=1\)
よって
\(α\bar{β}+\bar{α}β=1\)・・・①
ゆえに
\(|2β-α|^2\)
\(=4|β|^2-2(α\bar{β}+\bar{α}β)+|α|^2\)
\(=4-2+1\)
\(=3\)
だから
\(|2β-α|=\sqrt{3}\)
(2)
(1)より
\(α\bar{β}+\bar{α}β=1\)・・・①
\(|α|^2=|β|^2=1\) より
\(α\bar{α}=1\)、\(β\bar{β}=1\)
だから
\(\bar{α}=\displaystyle\frac{1}{α}\)、\(\bar{β}=\displaystyle\frac{1}{β}\)
これらを①代入して
\(\displaystyle\frac{α}{β}+\displaystyle\frac{β}{α}=1\)
\(\displaystyle\frac{β}{α}=t\) とおくと
\(\displaystyle\frac{1}{t}+t=1\)
\(t^2-t+1=0\)
したがって
\(\displaystyle\frac{β}{α}=\displaystyle\frac{1±\sqrt{3}i}{2}\)
(例題2)
点\(z\)が
\(|z+1-\sqrt{3}i|=\sqrt{2}\)
を満たす図形上を動くとき、\(z\)の偏角\(θ\)の範囲を求めよ。ただし、\(0≦θ<2π\) とする。
(解答)
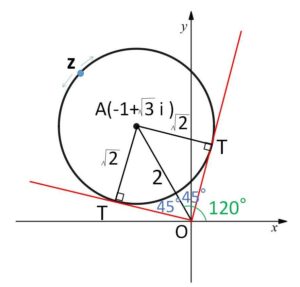
\(|z-(-1+\sqrt{3}i)|=\sqrt{2}\)
より、\(z\)は \(A(-1+\sqrt{3}i)\) を中心とする半径\(\sqrt{2}\)の円周上を動く。
\(O\)から円に接線を引き、接点を\(T\)とおくと
\(OA=2\)、\(AT=\sqrt{2}\)、\(OT \perp AT\) より
\(\angle AOT=\displaystyle\frac{π}{4}\)
また、\(\arg(-1+\sqrt{3}i)=\displaystyle\frac{2π}{3}\) だから
\(θ\)の最小値は
\(θ=\displaystyle\frac{2π}{3}-\displaystyle\frac{π}{4}=\displaystyle\frac{5π}{12}\)
\(θ\)の最大値は
\(θ=\displaystyle\frac{2π}{3}+\displaystyle\frac{π}{4}=\displaystyle\frac{11π}{12}\)
したがって\(θ\)のとりうる範囲は
\(\displaystyle\frac{5π}{12}≦θ≦\displaystyle\frac{11π}{12}\)
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→円の方程式と極形式 back→角の2等分線と複素数