円周上を動く点の極形式による表示方法について見ていきます。
・円の方程式と極形式
(原点中心の円)
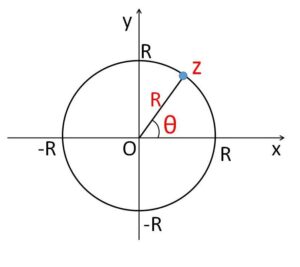
複素数平面上にある点\(z\)が原点を中心とする半径\(R\)の円周上を動くとき、つまり
\(|z|=R\)・・・①
を満たすとき、\(z\)を極形式で表すと次のようになります。
\(z=R(\cosθ+i\sinθ)\)・・・②
実際②を①の左辺に代入すると成り立ちます。
(一般的な円)
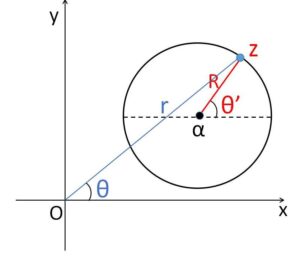
点\(z\)が点\(α\)を中心とする半径\(R\)の円周上を動くとき、つまり
\(|z-α|=R\)・・・③
を満たすとき、\(z\)を次のような形で表すことが可能です。
\(z=R(\cosθ’+i\sinθ’)+α\)・・・④
実際④を③の左辺に代入すると成り立ちます。
ところで、③を満たすように点\(z\)が動くときも、通常の極形式
\(z=r(\cosθ+i\sinθ)\)・・・⑤
で表すこともありますが、このとき図を参照してみると分かる通り、\(R,r\) や \(θ’,θ\) は基本的には一致しません。
また、⑤を③に代入すると\(r\)と\(θ\)の関係式が得られるので(極方程式)、⑤で表す場合も実質1変数による表示になります。
(例題1)
複素数\(z\)の絶対値が\(1\)であるとき、\(\sqrt{3}+i+z\) の絶対値を最大にする複素数\(z\)を求めよ。
(解答)
\(|z|=1\) より
\(z=\cosθ+i\sinθ\) (\(0≦θ<2π\)) と表せる。
このとき
\(|\sqrt{3}+i+z|^2\)
\(=|(\cosθ+\sqrt{3})+(\sinθ+1)i|^2\)
\(=(\cosθ+\sqrt{3})^2+(\sinθ+1)^2\)
\(=(\cos^2θ+2\sqrt{3}\cosθ+3)+(\sin^2θ+2\sinθ+1)\)
(\(\cos^2θ+\sin^2θ=1\) より)
\(=2(\sinθ+\sqrt{3}\cosθ)+5\)
(合成すると)
\(=4\sin(θ+\displaystyle\frac{π}{3})+5\)
よって \(\sqrt{3}+i+z\) の絶対値が最大のとき
\(θ+\displaystyle\frac{π}{3}=\displaystyle\frac{π}{2}\) だから
\(θ=\displaystyle\frac{π}{6}\)
したがって
\(z=\cos\displaystyle\frac{π}{6}+i\sin\displaystyle\frac{π}{6}\)
\(=\displaystyle\frac{\sqrt{3}}{2}+\displaystyle\frac{1}{2}i\)
(例題2)
複素数\(z\)は \(|z-1|=1\) をみたし、\(z^3\)は実数になるという。\(z\)を求めよ。
(解答)
\(|z-1|=1\) より
\(z=(\cosθ+i\sinθ)+1\) (\(0≦θ<2π\))
とおける。
このとき
\(z^3=\{(\cosθ+1)+i\sinθ\}^3\)
であり、虚部は
\(3(\cosθ+1)^2\sinθ-\sin^3θ\)
\(=\sinθ\{3(\cosθ+1)^2-\sin^2θ\}\)
\(=\sinθ\{3(\cosθ+1)^2-1+\cos^2θ\}\)
\(=\sinθ(4\cos^2θ+6\cosθ+2)\)
\(=2\sinθ(2\cosθ+1)(\cosθ+1)\)
よって\(z^3\)は実数のとき虚部は\(0\)だから
\(θ=0,\displaystyle\frac{2π}{3},\displaystyle\frac{4π}{3},π\)
したがって
\(z=(\cosθ+i\sinθ)+1\) より
\(z=2,\displaystyle\frac{1±\sqrt{3}i}{2},0\)
(別解)
\(z=r(\cosθ+i\sinθ)\) (\(r≧0\)、\(0≦θ<2π\)) とおくと
\(z^3=r^3(\cos3θ+i\sin3θ)\) より、\(z^3\)が実数になるとき
\(r=0\)、\(3θ=0,π,2π,3π,4π,5π\)
よって
\(z=0\)、\(θ=0,\displaystyle\frac{π}{3},\displaystyle\frac{2π}{3},π,\displaystyle\frac{4π}{3},\displaystyle\frac{5π}{3}\)
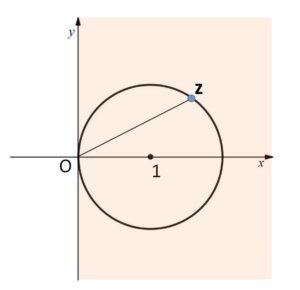
ここで、\(z≠0\) (\(r>0\)) のとき
\(|z-1|=1\)・・・①
が点\(1\)を中心とする半径\(1\)の円周を表すことから
\(0≦θ<\displaystyle\frac{π}{2}\)、\(\displaystyle\frac{3π}{2}<θ<2π\)
に限定できる。ゆえに
\(θ=0,\displaystyle\frac{π}{3},\displaystyle\frac{5π}{3}\)
となるから
\(z=r,\ r(\displaystyle\frac{1}{2}+\displaystyle\frac{\sqrt{3}i}{2}),\ r(\displaystyle\frac{1}{2}-\displaystyle\frac{\sqrt{3}i}{2})\)
(ア)
\(z=r\) を①に代入して
\(|r-1|=1\)
\(r>0\) より \(r=2\)
このとき \(z=2\)
(イ)
\(z=r(\displaystyle\frac{1}{2}+\displaystyle\frac{\sqrt{3}i}{2})\) を①に代入して
\(\left|r(\displaystyle\frac{1}{2}+\displaystyle\frac{\sqrt{3}i}{2})-1\right|=1\)
\(\left|(\displaystyle\frac{1}{2}r-1)+\displaystyle\frac{\sqrt{3}r}{2}i\right|^2=1^2\)
\((\displaystyle\frac{1}{2}r-1)^2+\displaystyle\frac{3r^2}{4}=1\)
整理して
\(r(r-1)=0\)
\(r>0\) より \(r=1\) だから
\(z=\displaystyle\frac{1}{2}+\displaystyle\frac{\sqrt{3}i}{2}\)
(ウ)
\(z=r(\displaystyle\frac{1}{2}-\displaystyle\frac{\sqrt{3}i}{2})\) を①に代入して
\(\left|r(\displaystyle\frac{1}{2}-\displaystyle\frac{\sqrt{3}i}{2})-1\right|=1\)
\(\left|(\displaystyle\frac{1}{2}r-1)-\displaystyle\frac{\sqrt{3}r}{2}i\right|^2=1^2\)
以下(イ)と同様になり
\(r=1\) だから
\(z=\displaystyle\frac{1}{2}-\displaystyle\frac{\sqrt{3}i}{2}\)
以上より
\(z=0,2,\displaystyle\frac{1}{2}±\displaystyle\frac{\sqrt{3}i}{2}\)
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→共円条件 back→図形と複素数の対応関係