複素数を利用したある点の位置の極限に関する例題です。
(例題)
平面上ではじめに座標の原点にあった動点\(P\)が、\(x\)軸の正方向に\(1\)だけ進む。次に進行方向に向かって左へ\(\displaystyle\frac{π}{6}\)だけ向きを変えて、\(\displaystyle\frac{1}{2}\) だけ進む。次に進行方向を左へさらに\(\displaystyle\frac{π}{6}\)変えて、\(\displaystyle\frac{1}{4}\)だけ進む。以下同じように、進行方向を左へ\(\displaystyle\frac{π}{6}\)ずつ変え、進む距離を前回の半分にしていくとき、動点\(P\)の極限の位置を求めよ。
複素数の数列の極限(和の極限)になりますが、通常の数列の極限と大まかには同じです。
(解答)
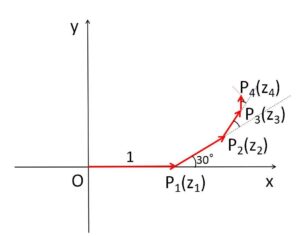
原点を\(P_0(z_0)\)、向きを変える点を \(P_1(z_1),P_2(z_2),\cdots,P_n(z_n)\) とおく。
題意より \(\overrightarrow{P_{n-1}P_{n}}\) を\(\displaystyle\frac{π}{6}\) 回転し、\(\displaystyle\frac{1}{2}\) 倍すると、\(\overrightarrow{P_{n}P_{n+1}}\) なる。
そこで
\(α=\displaystyle\frac{1}{2}(\cos\displaystyle\frac{π}{6}+i\sin\displaystyle\frac{π}{6})\)
とおいて
\(\overrightarrow{OP_{n}}=\overrightarrow{OP_1}+\overrightarrow{P_1P_2}+\overrightarrow{P_2P_3}+\cdots+\overrightarrow{P_{n-1}P_n}\)
を複素数で表すと
\(z_n=1+α+α^2+\cdots+α^{n-1}\)
\(=\displaystyle\frac{1-α^n}{1-α}\)
\(α^n=\displaystyle\frac{1}{2^n}(\cos\displaystyle\frac{nπ}{6}+i\sin\displaystyle\frac{nπ}{6})\)
より、三角関数の部分は大きさ1のままぐるぐる回転するだけなので、\(\displaystyle\frac{1}{2^n} \to 0\) より、\(α^n \to 0\) となります。
ここで
\(α^n=\displaystyle\frac{1}{2^n}(\cos\displaystyle\frac{nπ}{6}+i\sin\displaystyle\frac{nπ}{6})\)
だから
\(|α^n|=\displaystyle\frac{1}{2^n}\)
\(\displaystyle\lim_{n \to \infty}|α^n|=0\) となるので
\(\displaystyle\lim_{n \to \infty}α^n=0\)
よって
\(\displaystyle\lim_{n \to \infty}z_n=\displaystyle\frac{1}{1-α}\)
\(=\displaystyle\frac{1}{1-\displaystyle\frac{1}{2}(\displaystyle\frac{\sqrt{3}}{2}+\displaystyle\frac{1}{2}i)}\)
(分母分子4倍)
\(=\displaystyle\frac{4}{(4-\sqrt{3})-i}\)
(分母の実数化)
\(=\displaystyle\frac{4(4-\sqrt{3}+i)}{(4-\sqrt{3})^2+1}\)
\(=\displaystyle\frac{(4-\sqrt{3})+i}{5-2\sqrt{3}}\)
(有理化)
\(=\displaystyle\frac{\{(4-\sqrt{3})+i\}(5+2\sqrt{3})}{25-12}\)
\(=\displaystyle\frac{14+3\sqrt{3}}{13}+\displaystyle\frac{5+2\sqrt{3}}{13}i\)
したがって点\(P\)の極限の位置は
座標 \((\displaystyle\frac{14+3\sqrt{3}}{13},\displaystyle\frac{5+2\sqrt{3}}{13})\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→漸化式と複素数 back→共円条件