円の方程式

複素数平面における円の方程式の表現方法について見ていきます。

・円の方程式(複素数平面)
(1)基本形

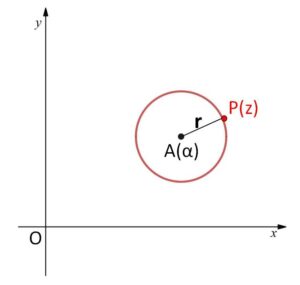
中心を \(α\) (定点) とする半径 \(r\) (\(r>0\)) の円の方程式は、\(P(z)\)と\(A(α)\)の距離が\(r\)であることから

\(|z-α|=r\)・・・①

とくに原点を中心とする円は、\(α=0\) として
\(|z|=r\)
となります。

(2)直径型

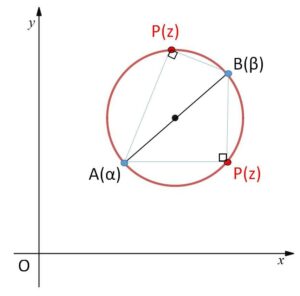
異なる2定点\(A(α),B(β)\)を結ぶ線分\(AB\)を直径とする円の方程式は、中心が \(\displaystyle\frac{α+β}{2}\)、半径は直径\(|α-β|\)の半分になるので、円周上の点を\(P(z)\)とすれば

\(\left|z-\displaystyle\frac{α+β}{2}\right|=\displaystyle\frac{|α-β|}{2}\)・・・②

または \(z≠α,β\) のとき、直径に対する円周角が\(\displaystyle\frac{π}{2}\)になることを利用すると、\(A,B\)から見こむ角が\(±\displaystyle\frac{π}{2}\)となるので、

\(\arg\displaystyle\frac{β-z}{α-z}=±\displaystyle\frac{π}{2}\)

よって、\(\displaystyle\frac{β-z}{α-z}\) は純虚数となるから、円の方程式は

\(\left(\displaystyle\frac{β-z}{α-z}\right)=-\overline{\left(\displaystyle\frac{β-z}{α-z}\right)}\)・・・③
(③は\(z=β\)を含めることもできる。さらに分母をはらえば \(z=α\)も含めることができる)

と表すこともできます。②③は変形すると同じ式になります。

(3)アポロ二ウスの円型

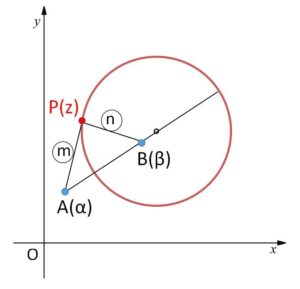
\(m,n\)を正の数 (\(m≠n\))とします。異なる2定点\(A(α),B(β)\)からの距離の比が \(m:n\) となる点\(P(z)\)の軌跡は円(アポロ二ウスの円という。数Ⅱ)になります。その方程式は
\(|z-α|:|z-β|=m:n\) より

\(n|z-α|=m|z-β|\)・・・④

実際④を2乗して展開整理して、再び絶対値の形にすると基本形①に帰着させることができます。
なお、\(m=n\) の場合は\(P(z)\)の軌跡は垂直2等分線(直線)になりますが、これは次回で扱いたいとお見ます。

円の方程式①～④は、絶対値が含まれる①②④については2乗して展開整理することで次のような形に変形することができ、これを円の方程式の一般形と呼びます。

\(az\bar{z}+\bar{β}z+β\bar{z}+c=0\)
(\(a\)は\(0\)でない実数、\(c\)は実数、\(β\)は複素数)

例えば
\(|z-α|=r\)・・・①  では
\(|z-α|^2=r^2\)
\((z-α)\overline{(z-α)}=r^2\)
\(z\bar{z}-\bar{α}z-α\bar{z}+|α|^2-r^2=0\)
となるので、\(a=1\)、\(-α=β\)、\(|α|^2-r^2=c\) とすれば上記一般形になります。

ただし、実数平面のときに
\(x^2+y^2+4=0\)
が円の方程式を表さない(半径が正の数としてとれない)ように、上記一般形でも円を表すために半径\(r\)が正の数でとれるような条件は必要です。(\(|β|^2>ac\))

以上が複素数平面における円の方程式の表現方法ですが、困ったら時には \(x+yi\) とおいて慣れ親しんだ直交座標に変換することも重要です。

(例題)
点\(z\)が
\(|z+3-\sqrt{3}i|=\sqrt{2}|z+2-\sqrt{3}i|\)
を満たす図形上を動くとき、\(|z|\)の最大値を求めよ。

(解答)
\(|z+3-\sqrt{3}i|=\sqrt{2}|z+2-\sqrt{3}i|\)
2乗して
\(|z+3-\sqrt{3}i|^2=2|z+2-\sqrt{3}i|^2\)
\((z+3-\sqrt{3}i)(\bar{z}+3+\sqrt{3}i)=2\{(z+2-\sqrt{3}i)(\bar{z}+2+\sqrt{3}i)\}\)
整理して
\(z\bar{z}+(1+\sqrt{3}i)z+(1-\sqrt{3}i)\bar{z}+2=0\)
(絶対値の形にする。因数分解すればよい)
\((z+1-\sqrt{3}i)(\bar{z}+1+\sqrt{3}i)-4+2=0\)
\((z+1-\sqrt{3}i)\overline{(z+1-\sqrt{3}i)}=2\)
\(|z+1-\sqrt{3}i|^2=2\)
よって
\(|z-(-1+\sqrt{3}i)|=\sqrt{2}\)
となり、点\(z\)は「中心を 点\(-1+\sqrt{3}i\) とする半径\(\sqrt{2}\)の円」を描く。

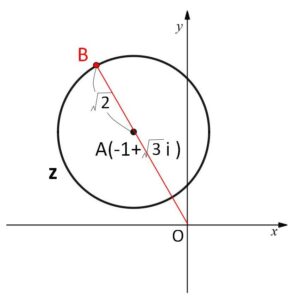
\(A(-1+\sqrt{3}i)\)とおく。直線\(OA\)と円の交点のうち\(O\)から遠い方を点\(B\)とおくと、\(OB\)が\(|z|\)の最大値\(|z|_{Max}\)になるから
\(|z|_{Max}=OB=OA+AB\)
\(=2+\sqrt{2}\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→直線の方程式　back→図形問題の証明と複素数