複素数平面における直線の方程式の表現方法について見ていきます。
・直線の方程式
(1)垂直2等分線
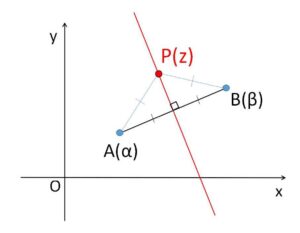
異なる2定点 \(A(α),B(β)\)があるとき、線分\(AB\)の垂直2等分線を表す方程式は、垂直2等分線上の点を\(P(z)\)とおくと、\(AP=BP\)より
\(|z-α|=|z-β|\)・・・①
(2)平行型
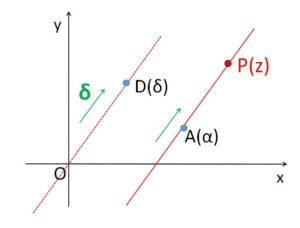
定点 \(A(α)\) を通り、\(0\)でない複素数\(δ\) (表す点は\(D(δ)\)とする) が表す方向に平行な直線の方程式は、直線上の点を\(P(z)\)とおくと 「\(AP /\!/ OD\) または \(A=P\) (\(A,P\)が一致)」だから、\(k\)を実数とすると
\(z-α=kδ\)・・・② (表現方法1)
②より
\(\displaystyle\frac{z-α}{δ}=k\) (実数)
となるから、次のように表すこともできます。
\(\displaystyle\frac{z-α}{δ}=\overline{\left(\displaystyle\frac{z-α}{δ}\right)}\)・・・③ (表現方法2)
(3)垂直型
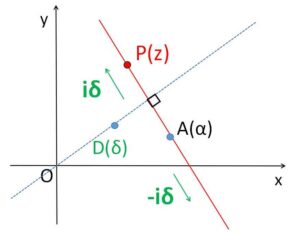
定点 \(A(α)\) を通り、\(0\)でない複素数\(δ\) (表す点は\(D(δ)\)とする) が表す方向に垂直な直線の方程式は、直線上の点を\(P(z)\)とおくと「\(AP \perp OD\) または \(A=P\) (\(A,P\)が一致)」だから、\(k\)を実数とすると
\(z-α=kδi\)・・・④ (表現方法1)
④より
\(\displaystyle\frac{z-α}{δ}=ki\) (純虚数または\(0\))
となるので、次のように表すこともできます。
\(\displaystyle\frac{z-α}{δ}=-\overline{\left(\displaystyle\frac{z-α}{δ}\right)}\)・・・⑤ (表現方法2)
円の接線の方程式なども同様の考え方で求めることが可能です。
(4)異なる2点型
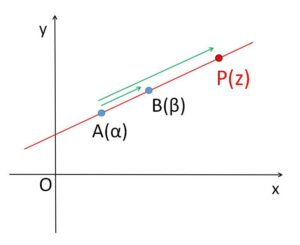
異なる2定点 \(A(α),B(β)\) を通る直線の方程式は、直線上の点を\(P(z)\)、\(k\)を実数とすると「\(AP /\!/ AB\) または \(A=P\)」なので
\(z-α=k(β-α)\)・・・⑥ (表現方法1)
⑥より
\(\displaystyle\frac{z-α}{β-α}=k\) (実数)
となるから、次のように表すこともできます。
\(\displaystyle\frac{z-α}{β-α}=\overline{\left(\displaystyle\frac{z-α}{β-α}\right)}\)・・・⑦ (表現方法2)
\(z,α,β\)が一直線上にある条件(共線条件)として⑦をいきなり導いても構いません。また上式では\(α\)を基準にしましたが、\(β\)を基準としても大丈夫です。
直線の方程式①③⑤⑦を式変形(①については2乗して展開整理)すると、次の直線の方程式の一般形にまとめることができることが分かります。
\(\bar{β}z+β\bar{z}+c=0\)
(\(β\)は\(0\)でない複素数、\(c\)は実数)
円の方程式の一般形と似ていますが大きく違うのは、\(z\bar{z} \ (|z|^2)\) の項がないところ(つまり1次式)です。
また直線の方程式も同様に(一般的な複素数の方程式も同様)、困ったら \(x+yi\) とおいて実数の座標平面に変換することも大切です。
(例題)
\(iz-i\bar{z}=1\) を満たす\(z\)は、複素数平面上でどのような図形を描くか。
(解答)
\(z=x+yi\) とおくと
\(i(x+yi)-i(x-yi)=1\)
整理して
\(-2y=1\)
\(y=-\displaystyle\frac{1}{2}\)
よって、点\(-\displaystyle\frac{1}{2}i\)を通る実軸に平行な直線。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→垂心・垂線の足と複素数 back→円の方程式