複素数の垂心や垂線の足に関する例題です。
(例題)
複素数平面上の原点を中心とする半径\(1\)の円\(C\)上に相異なる3点\(z_1,z_2,z_3\)をとる。次の問いに答えよ。
(1)\(ω_1=z_1+z_2+z_3\) とおく。点\(ω_1\)は3点\(z_1,z_2,z_3\)を頂点とする三角形の垂心になることを示せ。ここで、三角形の垂心とは、各頂点から対辺またはその延長線上に下ろした3本の垂線の交点のことであり、これらの3本の垂線は1点で交わることが知られている。
(2)\(ω_2=-\bar{z_1}z_2z_3\) とおく。\(ω_2≠z_1\) のとき、2点\(z_2,z_3\)を通る直線上に\(z_1\)から下ろした垂線またはその延長線が円\(C\)と交わる点は\(ω_2\)であることを示せ。ここで、\(\bar{z_1}\)は\(z_1\)に共役な複素数である。
(3)2点\(z_2,z_3\)を通る直線とこの直線上に\(z_1\)から下ろした垂線との交点は、点\(ω_1\)と点\(ω_2\)を結ぶ線分の中点であることを示せ。ただし、\(ω_1=ω_2\) のときは、\(ω_1\)と\(ω_2\)の中点は\(ω_1\)と解釈する。
もちろん、これらの点が単位円 \(|z|=1\) 上にあることは各所で用います。
(解答)
(1)
垂直であること示すには、商が純虚数であることを示せばよいですが、三角形が直角三角形の場合には垂心が1頂点と一致し、この場合3つの商のうち1つが\(0\)(実数)になるために、念のため場合分けしておきます。
(ア)\(ω_1\)が3頂点\(z_1,z_2,z_3\)のいずれにも一致しないとき
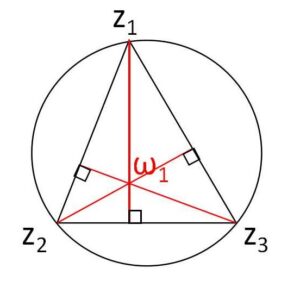
まず、\(ω_1-z_1 \perp z_3-z_2\) を示す。
\(\displaystyle\frac{ω_1-z_1}{z_3-z_2}+\overline{\left(\displaystyle\frac{ω_1-z_1}{z_3-z_2}\right)}\)
\(=\displaystyle\frac{z_3+z_2}{z_3-z_2}+\displaystyle\frac{\bar{z_3}+\bar{z_2}}{\bar{z_3}-\bar{z_2}}\)
\(=\displaystyle\frac{2(|z_3|^2-|z_2|^2)}{(z_3-z_2)(\bar{z_3}-\bar{z_2})}\)
\(=0\) (\(|z_2|=|z_3|=1\) より)
よって \(\displaystyle\frac{ω_1-z_1}{z_3-z_2}\) は純虚数だから
\(ω_1-z_1 \perp z_3-z_2\)
同様に
\(ω_1-z_2 \perp z_3-z_1\)
\(ω_1-z_3\perp z_2-z_1\)
も示せるので、\(ω_1\)は垂心となる。
(イ)\(ω_1\)が3頂点\(z_1,z_2,z_3\)のいずれかに一致するとき
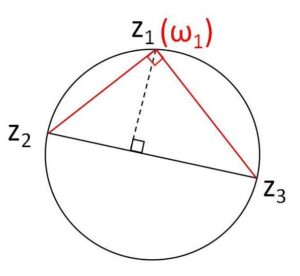
例えば \(ω_1=z_1\) のとき、(ア)より
\(ω_1-z_2 \perp z_3-z_1\)
\(ω_1-z_3\perp z_2-z_1\)
だから、頂点\(z_1\)の角は直角。よって、\(ω_1 \ (z_1)\) は垂心となる。
\(ω_1=z_2またはz_3\) の場合も同様。
(2)
\(z\)について解く際には、\(z_1\)も円と垂線の交点であることから解としてでてくることを意識するとよいです。
もしくは、\(ω_2\)が円の方程式と垂線の方程式を満たすことを示してもよいです。
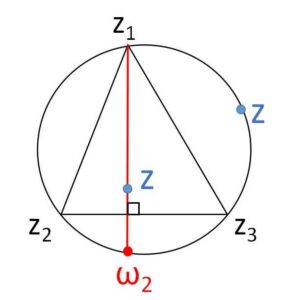
\(z_1\)から直線\(z_2z_3\)へ下ろした垂線の方程式は、\(z-z_1 \perp z_3-z_2\) または \(z=z_1\) より
\(\displaystyle\frac{z-z_1}{z_3-z_2}=-\overline{\left(\displaystyle\frac{z-z_1}{z_3-z_2}\right)}\)
分母をはらって左辺に寄せると
\((z-z_1)(\bar{z_3}-\bar{z_2})+(\bar{z}-\bar{z_1})(z_3-z_2)=0\)・・・(i)
(この形のまま進めてもよいですが、(3)も踏まえて \(\bar{z_1},\bar{z_2},\bar{z_3}\) を消去して整理します)
\(z_1,z_2,z_3\) は、\(|z|=1\) つまり \(z\bar{z}=1\) 上の点だから
\(\bar{z_1}=\displaystyle\frac{1}{z_1}\)、\(\bar{z_2}=\displaystyle\frac{1}{z_2}\)、\(\bar{z_3}=\displaystyle\frac{1}{z_3}\)
よって(i)は
\((z-z_1)(\displaystyle\frac{1}{z_3}-\displaystyle\frac{1}{z_2})+(\bar{z}-\displaystyle\frac{1}{z_1})(z_3-z_2)=0\)
\(\displaystyle\frac{z_2-z_3}{z_2z_3}\left\{(z-z_1)-z_2z_3(\bar{z}-\displaystyle\frac{1}{z_1})\right\}=0\)
\(z_2≠z_3\) より
\((z-z_1)-z_2z_3(\bar{z}-\displaystyle\frac{1}{z_1})=0\)・・・①
単位円の方程式は
\(|z|=1\)
\(z\bar{z}=1\)・・・②
①②の交点のうち\(z_1\)でないものが\(ω_2\)である。
②より \(\bar{z}=\displaystyle\frac{1}{z}\)
これを①に代入して
\((z-z_1)-z_2z_3(\displaystyle\frac{1}{z}-\displaystyle\frac{1}{z_1})=0\)
\(\displaystyle\frac{z-z_1}{zz_1}(zz_1+z_2z_3)=0\)
\(z≠z_1\) より
\(z=-\displaystyle\frac{z_2z_3}{z_1}\)\(=-\bar{z_1}z_2z_3\)
したがって
\(ω_2=-\bar{z_1}z_2z_3\) は垂線と円の交点。
(3)
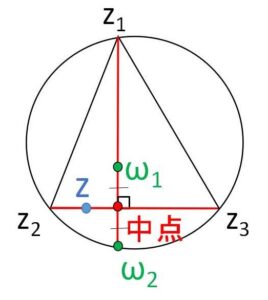
直線\(z_2z_3\)の方程式は、\(z-z_2 /\!/ z_3-z_2\) または \(z=z_2\) より
\(\displaystyle\frac{z-z_2}{z_3-z_2}=\overline{\left(\displaystyle\frac{z-z_2}{z_3-z_2}\right)}\)
よって
\((z-z_2)(\bar{z_3}-\bar{z_2})-(\bar{z}-\bar{z_2})(z_3-z_2)=0\)
\((z-z_2)(\displaystyle\frac{1}{z_3}-\displaystyle\frac{1}{z_2})-(\bar{z}-\displaystyle\frac{1}{z_2})(z_3-z_2)=0\)
\(\displaystyle\frac{z_2-z_3}{z_2z_3}\left\{(z-z_2)+z_2z_3(\bar{z}-\displaystyle\frac{1}{z_2})\right\}=0\)
\(z_2≠z_3\) より
\(z-z_2+z_2z_3\bar{z}-z_3=0\)・・・③
(2)の①より\(z_1\)から下ろした垂線の方程式は
\((z-z_1)-z_2z_3(\bar{z}-\bar{z_1})=0\)
\(z-z_1-z_2z_3\bar{z}+\bar{z_1}z_2z_3=0\)・・・①’
③と①’の交点は、③+①’ より \(\bar{z}\) を消去すると
\(2z-(z_1+z_2+z_3)+\bar{z_1}z_2z_3=0\)
したがって
\(z=\displaystyle\frac{z_1+z_2+z_2-\bar{z_1}z_2z_3}{2}=\displaystyle\frac{ω_1+ω_2}{2}\)
となるので、交点は\(ω_1,ω_2\)の中点である。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→内心・外心と複素数 back→直線の方程式