三角形の内心・外心の複素数による表現方法について見ていきます。
・三角形の内心(複素数)
複素数平面上にある三角形の内心を表す複素数は、内心が角の2等分線の交点であることを利用して求めることができます。
複素数平面上にある三角形\(ABC\)の内心を\(I\)とし、\(A(α),B(β),C(γ)\) とおきます。ひとまず3辺を \(BC=a,\ CA=b,\ AB=c\) として、これを用いて進めていき最終的に複素数で表すことにします。
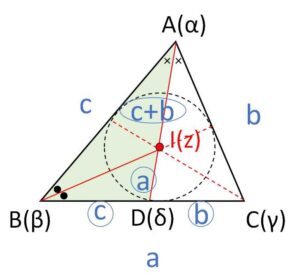
\(\angle A\) の2等分線と\(BC\)の交点を\(D(δ)\)とおくと、内角の2等分線の定理より\(D\)は\(BC\)を\(c:b\)に内分する点だから
\(δ=\displaystyle\frac{bβ+cγ}{c+b}\)
よって、内心\(I(z)\)は\(\angle B\)の2等分線と\(AD\)の交点だから内角の2等分線の定理を用いると
\(AI:ID=c:\displaystyle\frac{c}{c+b}a=(c+b):a\)
だから
\(z=\displaystyle\frac{aα+(c+b)\cdot\displaystyle\frac{bβ+cγ}{c+b}}{(c+b)+a}\)
\(=\displaystyle\frac{aα+bβ+cγ}{a+b+c}\)
(\(a,b,c\)を複素数で表して)
\(=\displaystyle\frac{|γ-β|α+|α-γ|β+|β-α|γ}{|γ-β|+|α-γ|+|β-α|}\)
・三角形の外心(複素数)
複素数平面上にある三角形の外心を表す複素数は、各辺の垂直2等分線の交点が外心であることから求めることができます。
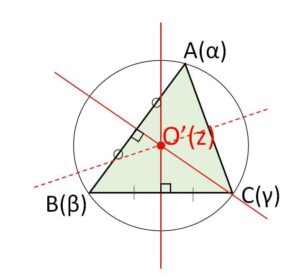
辺\(AB\)の垂直2等分線を表す方程式は
\(|z-α|=|z-β|\)・・・①
辺\(BC\)の垂直2等分線を表す方程式は
\(|z-β|=|z-γ|\)・・・②
直線①②の交点が外心を表す複素数なので、連立して交点を求めます(最終的に\(\bar{z}\)を消せばよい)。
①より
\(|z-α|^2=|z-β|^2\)
\((z-α)(\bar{z}-\bar{α})=(z-β)(\bar{z}-\bar{β})\)
整理して
\((\bar{β}-\bar{α})z+(β-α)\bar{z}=|β|^2-|α|^2\)・・・①’
同様に②より
\((\bar{γ}-\bar{β})z+(γ-β)\bar{z}=|γ|^2-|β|^2\)・・・②’
①’×(γ-β)-②’×(β-α) より
\((γ-β)(\bar{β}-\bar{α})z-(β-α)(\bar{γ}-\bar{β})z\)
\(=(γ-β)(|β|^2-|α|^2)-(β-α)(|γ|^2-|β|^2)\)
両辺整理して
\(\left\{\bar{α}(β-γ)+\bar{β}(γ-α)+\bar{γ}(α-β)\right\}z\)
\(=|α|^2(β-γ)+|β|^2(γ-α)+|γ|^2(α-β)\)
よって外心を表す複素数は
\(z=\displaystyle\frac{|α|^2(β-γ)+|β|^2(γ-α)+|γ|^2(α-β)}{\bar{α}(β-γ)+\bar{β}(γ-α)+\bar{γ}(α-β)}\)
もしくは、外接円の方程式を立式して解く方法もありますが、上記方法と途中から同じになります。
外接円の方程式は変数\(ω\)を使うと、中心\(z\)、半径\(r\)として
\(|ω-z|=r\)
\(A(α),B(β),C(γ)\)は、この円周上にあるので \(ω=α,β,γ\)を代入して
\(|α-z|=|β-z|=|γ-z|=r\)
左の3式を取り出せば①②になります。
(例題)
3点\(0,1,α\)を通る円の中心\(β\)を求めよ。またその円の方程式を求めよ。ただし、\(α\)は実数でないとする。
\(O(0),A(α),C(1)\) とおく。
\(OA\)の垂直2等分線の方程式は
\(|z|=|z-α|\)・・・①
\(OC\)の垂直2等分線の方程式は
\(|z|=|z-1|\)・・・②
①と②の交点が外心\(β\)である。
①より
\(|z|^2=|z-α|^2\)
\(z\bar{z}=(z-α)(\bar{z}-\bar{α})\)
よって
\(\bar{α}z+α\bar{z}=|α|^2\)・・・①’
同様に②より
\(|z|^2=|z-1|^2\) だから
\(z+\bar{z}=1\)・・・②’
①’-②’×α より \(\bar{z}\) を消去すると
\((\bar{α}-α)z=|α|^2-α\)
\(α\)は実数ではないので、\(\bar{α}-α≠0\) だから
\(z=\displaystyle\frac{α-|α|^2}{α-\bar{α}}\)
したがって
\(β=\displaystyle\frac{α-|α|^2}{α-\bar{α}}\)
また、円が\(0\)を通るので半径は\(|β|\)となるから、円の方程式は
\(|z-β|=|β|\) より
\(\left|z-\displaystyle\frac{α-|α|^2}{α-\bar{α}}\right|=\left|\displaystyle\frac{α-|α|^2}{α-\bar{α}}\right|\)
(注)
\(α\)が実数でない条件は分母が\(0\)にならないことに使いましたが、そもそも\(α\)が実数だと3点\(0,1,α\)が1直線上に並んでしまうので、3点を通る円が存在しません。
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→対称移動と複素数 back→垂心・垂線の足と複素数