\(x+yi\) とおく複素数平面の領域の例題です。
(例題)
\(0\)でない複素数\(z\)に対し
\(w=z^2-\displaystyle\frac{1}{z^2}\)
とおく。このとき、\(w\)の実部が正になるような\(z\)の範囲を複素数平面上に図示せよ。
(解答)
\(z=x+yi\) (\((x,y)≠(0,0)\)) とおく。
\(w=z^2-\displaystyle\frac{1}{z^2}\)
\(=(x+yi)^2-\displaystyle\frac{1}{(x+yi)^2}\)
\(=(x+yi)^2-\displaystyle\frac{(x-yi)^2}{(x+yi)^2(x-yi)^2}\)
\(=(x+yi)^2-\displaystyle\frac{(x-yi)^2}{(x^2+y^2)^2}\)
よって\(w\)の実部\(Re(w)\)は
\(Re(w)=(x^2-y^2)-\displaystyle\frac{x^2-y^2}{(x^2+y^2)^2}\)
\(=(x^2-y^2)\left\{1-\displaystyle\frac{1}{(x^2+y^2)^2}\right\}\)
\(=(x^2-y^2)\cdot\displaystyle\frac{(x^2+y^2)^2-1}{x^2+y^2}\)
\(=\displaystyle\frac{(x^2-y^2)(x^2+y^2+1)(x^2+y^2-1)}{x^2+y^2}\)
(\(x^2+y^2>0,\ x^2+y^2+1>0\) より2つの積のみ着目すればよい)
\(Re(w)>0\) より
\((x^2-y^2)(x^2+y^2-1)>0\)
つまり
\((x-y)(x+y)(x^2+y^2-1)>0\)
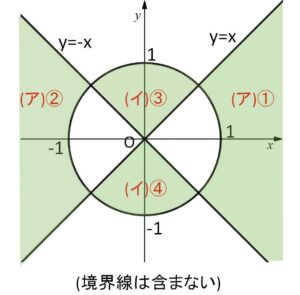
(ア)\(x^2+y^2-1>0\) のとき (円の外側のとき)
\((x-y)(x+y)>0\)
つまり
\(x-y>0\) かつ \(x+y>0\)・・・①
または
\(x-y<0\) かつ \(x+y<0\)・・・②
(イ)\(x^2+y^2-1<0\) のとき (円の内側のとき)
\((x-y)(x+y)<0\)
つまり
\(x-y<0\) かつ \(x+y>0\)・・・③
または
\(x-y>0\) かつ \(x+y<0\)・・・④
\(z\)の範囲は、(ア)(イ)を図示することにより次の通りになる。( \((x,y)=(0,0)\) を満たす)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→線分上を動く点と軌跡・領域 back→複素数平面と領域①(基本形・逆像型)