今回からベクトルについて学んでいきます。
まずは比較的分かりやすい平面におけるベクトルから考えていきます。(今回学ぶことは空間におけるベクトルでも成り立ちますが、最初は平面で考えたほうが分かりやすいと思います)
・ベクトルの導入
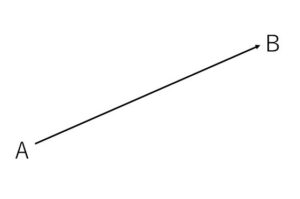
点\(A\)から点\(B\)までの移動は、図のように線分\(AB\)に向きを示す矢印をつけて表すことができます。このように向きのついた線分を有向線分といいます。
ここで有向線分でその位置を問題にしないで、向きと長さ(大きさ)だけに着目したものをベクトルとといいます。
またベクトルは位置を問題にしません。位置を問題にしないほうが便利なことが多いからですが、位置まで考慮したベクトル(位置ベクトル)もあります。
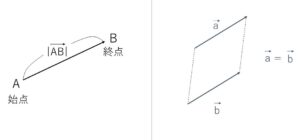
有向線分\(AB\)と同じ向き、大きさをもったベクトルを \(\overrightarrow{AB}\) と書きます。
(\(\vec{a}\) のように1文字で表す場合もあります)
また、\(A\)を始点、\(B\)を終点といい、\(\overrightarrow{AB}\) の大きさ(長さを)\(|\overrightarrow{AB}|\) で表します。特に大きさが\(1\)であるベクトルを単位ベクトルといいます。
位置を問題にしないので、2つのベクトル\(\vec{a}\),\(\vec{b}\)の一方を平行移動させて他方にぴったり重ね合わせることができる場合、この2つのベクトルは等しいといい、\(\vec{a}=\vec{b}\) で表します。
・逆ベクトル・零ベクトル
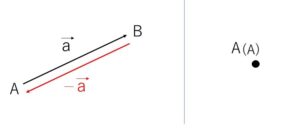
ベクトル\(\vec{a}\)と大きさが同じで向きが反対のベクトルを\(\vec{a}\)の逆ベクトルといい、\(-\vec{a}\) で表します。
\(\vec{a}=\overrightarrow{AB}\) とすると、\(-\vec{a}=\overrightarrow{BA}\) です。
また、始点と終点が一致したベクトル\(\overrightarrow{AA}\)を零ベクトルといい、\(\vec{0}\) で表します。\(\vec{0}\) の大きさは\(0\)で、向きは考えません。
・ベクトルの加法・減法
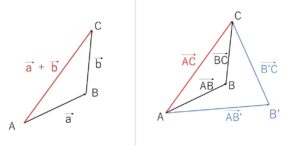
2つのベクトル\(\vec{a},\vec{b}\)についてベクトルの和を次のように定義します。
2つのベクトルを平行移動させて、一方の終点と他方の始点が一致するようにします。図のように点\(A,B,C\)を定めると、\(\overrightarrow{AC}\) を\(\vec{a},\vec{b}\)の和と定めて
\(\vec{a}+\vec{b}=\overrightarrow{AC}\)
とします。つまり
\(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\)・・・①
となります。
ここで仮に\(B\)を別の点\(B’\)にしても①式は成り立つので、一般化すると次の通りです。
\(\overrightarrow{A□}+\overrightarrow{□C}=\overrightarrow{AC}\)・・・②
(\(□\)は同じ点)
①式により\(A→B→C\) の移動と、\(A→C\) の移動が同じになっているので途中経路は関係ないことになります。
②式の(左辺)→(右辺)を考えると、2つのベクトルを合体させることができて、
(右辺)→(左辺)を考えると、1つのベクトルを適当な点で仲介させて和にすることができます。
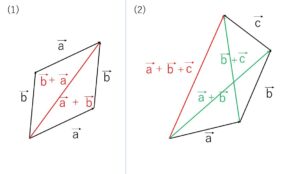
この和の定義により、ベクトルの加法について次のことが成り立ちます。
(2)\((\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})\) (結合法則)
(3)\(\vec{a}+\vec{0}=\vec{a}\)
(4)\(\vec{a}+(-\vec{a})=\vec{0}\)
(差にすると \(\vec{a}-\vec{a}=\vec{0}\))
(1)(2)は図より、(4)は逆ベクトルの定義から明らかです。
(3)は\(\vec{0}\)が何も移動しないと考えれば成り立つことが分かります。
また、ベクトルの差については次のように定義します。
\(\vec{a}-\vec{b}=\vec{a}+(-\vec{b})\)
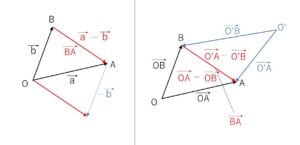
ここで、\(\vec{a}=\overrightarrow{OA}\), \(\vec{b}=\overrightarrow{OB}\) と定めると、図より
\(\vec{a}-\vec{b}=\overrightarrow{BA}\)
となるので
\(\overrightarrow{OA}-\overrightarrow{OB}=\overrightarrow{BA}\)・・・③
③式は\(O\)を別の点に置き換えても成り立つので、一般的に次の等式が成り立ちます。
\(\overrightarrow{□A}-\overrightarrow{□B}=\overrightarrow{BA}\)・・・④
(\(□\)は同じ点)
そして(右辺)→(左辺)が特に重要で、1つのベクトルを2つの差のベクトルに変換するもので、しかも始点をある\(□\)に統一できます。\(\overrightarrow{BA}=(□終点)-(□始点)\) と覚えるといいと思います。
・ベクトルの実数倍
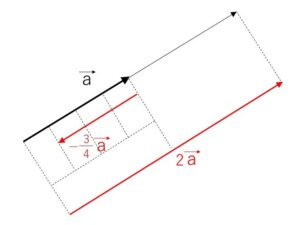
ベクトル\(\vec{a}\)と実数\(k\)について、ベクトルの実数倍 \(k\vec{a}\) を次のように定義します。
(ア)\(k>0\) のときは、\(\vec{a}\)と同じ向きで大きさが\(k\)倍のベクトル
(イ)\(k<0\) のときは、\(\vec{a}\)と反対の向きで大きさが\(|k|\)倍のベクトル
(ウ)\(k=0\) のときは、\(\vec{0}\)
したがって、\(k\vec{a}\) の大きさについて次の等式が成り立ちます。
\(|k\vec{a}|=|k||\vec{a}|\)
また、\(\vec{a}\) と同じ向きの単位ベクトルは、\(\vec{a}\)の大きさが \(|\vec{a}|\) であることから、\(\displaystyle\frac{\vec{a}}{|\vec{a}|}\) と表すことができます。
そして、ベクトルの実数倍においてもスカラー(普通の数)と同じように以下の法則が成り立ちます。
(5)\(k(l\vec{a})=(kl)\vec{a}\)
(6)\((k+l)\vec{a}=k\vec{a}+l\vec{a}\)
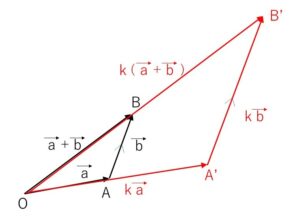
(7)\(k(\vec{a}+\vec{b})=k\vec{a}+k\vec{b}\)
(5)(6)については、ベクトルの実数倍の意味や図を考えれば成り立つことが分かります。
(7)については下図について、図形の相似に着目すればよいです。
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→ベクトルの演算と図示①