\(\require{cancel}\)
ベクトルの平行に関する演習です。
(例題1)
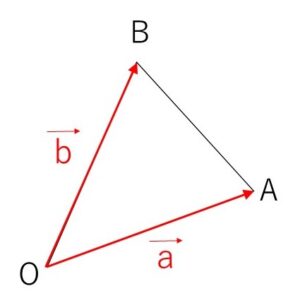
(1)\(△OAB\)において、\(\overrightarrow{OA}=\vec{a}\), \(\overrightarrow{OB}=\vec{b}\) とする。
\(\overrightarrow{OP}=3\vec{a}-2\vec{b}\), \(\overrightarrow{OQ}=3\vec{a}\) のとき \(PQ/\!/OB\) を示せ。
(2)\((2\vec{a}+3\vec{b})/\!/(\vec{a}-4\vec{b})\), \(\vec{a}≠0\), \(\vec{b}≠0\) のとき、\(\vec{a}/\!/\vec{b}\) であることを示せ。
また\(\vec{0}\)でないことも確認しておきます。
(解答)
(1)
それと解答では使いませんが、\(\vec{a}\bcancel{/\!/}\vec{b}\) (平行でない)です。
\(\overrightarrow{PQ}=\overrightarrow{OQ}-\overrightarrow{OP}\)
\(=3\vec{a}-(3\vec{a}-2\vec{b})\)
\(=2\vec{b}\)
よって
\(\overrightarrow{PQ}=2\overrightarrow{OB}\)
ここで \(\vec{b}≠0\) より
\(\overrightarrow{PQ}≠0\), \(\overrightarrow{OB}≠0\) となるので
\(PQ/\!/OB\)
(2)
\((2\vec{a}+3\vec{b})/\!/(\vec{a}-4\vec{b})\) より
\((2\vec{a}+3\vec{b})=k(\vec{a}-4\vec{b})\)
\((k-2)\vec{a}=(4k+3)\vec{b}\)
ここで、\(k=2\) とすると \(11\vec{b}=\vec{0}\) つまり \(\vec{b}=\vec{0}\) となるので不適。
よって \(k≠2\) で
\(\vec{a}=\displaystyle\frac{4k+3}{k-2}\vec{b}\)
\(\vec{a}≠0\), \(\vec{b}≠0\) より
\(\vec{a}/\!/\vec{b}\)
(例題2)
座標平面上に3定点\(A,B,C\)と動点\(P\)があって、\(\overrightarrow{AB}=(3,1)\), \(\overrightarrow{BC}=(1,2)\) であり、\(\overrightarrow{AP}\) が実数\(t\)を用いて \(\overrightarrow{AP}=(2t,3t)\) と表されるとき
(1)\(\overrightarrow{PC}\) を求めよ。
(2)\(\overrightarrow{PC}\) が \(\overrightarrow{AB}\) と平行であるときの\(t\)の値を求めよ。
(解答)
(1)
条件より\(\overrightarrow{AC}\) が求まり、
また、\(\overrightarrow{PC}=\overrightarrow{AC}-\overrightarrow{AP}\) です。
\(\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}\)
\(=(3,1)+(1,2)\)
\(=(4,3)\)
\(\overrightarrow{PC}=\overrightarrow{AC}-\overrightarrow{AP}\)
\(=(4,3)-(2t,3t)\)
\(=(4-2t,3-3t)\)
(2)
\(\overrightarrow{PC}/\!/\overrightarrow{AB}\) より
\((4-2t)\cdot1-(3-3t)\cdot3=0\)
\(-5+7t=0\)
よって
\(t=\displaystyle\frac{5}{7}\)
このとき
\(\overrightarrow{PC}=(\displaystyle\frac{18}{7},\displaystyle\frac{6}{7})≠\vec{0}\)
(例題3)
平面上の3点 \(A(t^2-2t-8,2t^2+t)\), \(B(3t^2+2t,t^2-t-4)\), \(C(t^2-8,2t^2)\) について、次の問いに答えよ。ただし、\(t\)は\(0\)でない実数とする。
(1)\(A,B,C\)は一直線上にあることを示せ。
(2)\(\overrightarrow{AC}=k\overrightarrow{AB}\) とおくとき、\(k\)の値の範囲を求めよ。
(3)\(A,B,C,D\)が、ある順序で等間隔に並んでいるとする。ただし、\(D\)は\(A,B,C\)と異なる点である。このとき\(t\)の値を求めよ。
(解答)
(1)
\(\overrightarrow{AC}=(t^2-8-(t^2-2t-8),2t^2-(2t^2+t))\)
\(=(2t,-t)\)
\(=t(2,-1)\)
\(\overrightarrow{AB}=(3t^2+2t-(t^2-2t-8),t^2-t-4-(2t^2+t))\)
\(=(2t^2+4t+8,-t^2-2t-4)\)
\(=(t^2+2t+4)(2,-1)\)
\(t^2+2t+4=(t+1)^2+3>0\) より
\(\overrightarrow{AC}=\displaystyle\frac{t}{t^2+2t+4}\overrightarrow{AB}\)
よって\(A,B,C\)は一直線上にある。
\(\overrightarrow{AC}=k\overrightarrow{AB}\) \(→\) \(A,B,C\)が一直線上にある
は\(A,B\)が一致していても成り立ちます(逆は成り立つとは限りません)。実際、\(A=B\) のときは右辺が\(\vec{0}\)になりますが、等式が成り立っているので左辺から\(A=C\)となり、3点が一致しているからです(このとき3点(1点)を通る直線は無数にある)。
なお本問は\(t≠0\), \(t^2+2t+4≠0\) なので、\(A,B,C\)は異なる3点です。
(2)
(1)より
\(k=\displaystyle\frac{t}{t^2+2t+4}\)・・・①
\(t^2+2t+4(≠0)\) を両辺に掛けて
\(k(t^2+2t+4)=t\)
\(t\)について整理して
\(kt^2+(2k-1)t+4k=0\)・・・②
「\(k\)に対応する\(t\)がある」という考え方が逆像法です(2次方程式②の実数解の存在を考える)。ただし、\(t≠0\) には注意します。
\(t\)の2次方程式②が\(t=0\)ではない実数解をもてばよいので、
\(D≧0\)
\((2k-1)^2-16k^2≧0\)
\(12k^2+4k-1≦0\)
\((6k-1)(2k+1)≦0\)
\(-\displaystyle\frac{1}{2}≦k≦\displaystyle\frac{1}{6}\)
また、\(t=0\) のとき②より \(k=0\) だから
\(k≠0\)
したがって
\(-\displaystyle\frac{1}{2}≦k<0\), \(0<k≦\displaystyle\frac{1}{6}\)
(3)
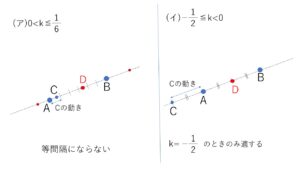
(ア)\(0<k≦\displaystyle\frac{1}{6}\) のときは \(A,C,B\) の順で並びますが、\(D\)をどの位置にいれても(特に\(C,B\)の間を考える)等間隔にはなりません。
(イ)\(-\displaystyle\frac{1}{2}≦k<0\) のときは \(C,A,B\) の順で並び、\(A,B\)の間に\(D\)を入れると、ちょうど\(k=-\displaystyle\frac{1}{2}\) のときのみが条件に適することが分かります。このとき\(D\)は\(A,B\)の中点です。
(2)より
\(-\displaystyle\frac{1}{2}≦k<0\), \(0<k≦\displaystyle\frac{1}{6}\)
4点が等間隔に並ぶのは
\(k=-\displaystyle\frac{1}{2}\) のときのみで、\(C,A,D,B\)の順に並ぶ。
②より
\(-\displaystyle\frac{1}{2}t^2-2t-2=0\)
\(t^2+4t+4=0\)
\((t+2)^2=0\)
よって
\(t=-2\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→平行四辺形とベクトル back→ベクトルの平行①