正五角形の性質について見ていきます。
・正五角形の性質
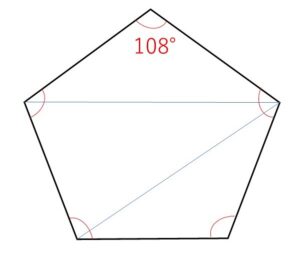
正五角形は、全ての辺の長さと全ての内角が等しい五角形です。
正五角形は対角線をひくことで3つの三角形に分割できるので、内角の総和が \(180°×3=540°\) となるので1つの内角は \(540÷5=\)\(108°\) となります。
正五角形には全部で5本の対角線をひくことができますが、ここから様々な特徴が表れます。
(1)\(36°\), \(72°\), \(108°\) の角度の登場
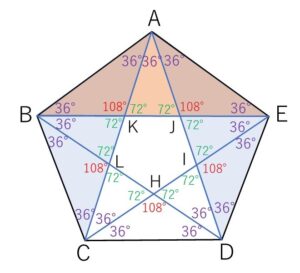
\(△ABE\) は\(AB=AE\) より 内角が \(108°,36°,36°\) の二等辺三角形。
同様に、\(△BCA\), \(△EAD\) も\(108°,36°,36°\) の二等辺三角形。
したがって \(\angle CAD=108°-(36°+36°)=36°\) であり、点\(A\)を通る対角線は \(\angle A\) を3等分しています。(他の頂点\(B,C,D,E\) も同様)
すると芋づる式に対角線で作られる他の角も\(72°\)や\(108°\)と求まります。
(2)合同 or 相似 の三角形の登場
(1)で求めた角度により、合同や相似である三角形が多数現れます。
(\(108°,36°,36°\)の三角形)
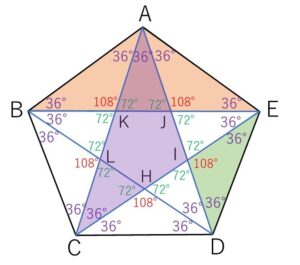
①まず2辺が正五角形の辺で、1辺が対角線である三角形(\(△ABE\)をはじめ全部で5個) は合同。
また、これらと合同な三角形は星型の図形の内部にもあります。(\(△IAC\)をはじめ全部で5個で、一辺が対角線なので合同)。
②次に1辺が正五角形の辺である三角形は\(△IDE\)をはじめ全部で5個。
一辺が正五角形の辺なのでこれらは合同となります。
①と②の三角形は相似です。
(\(36°,72°,72°\)の三角形)
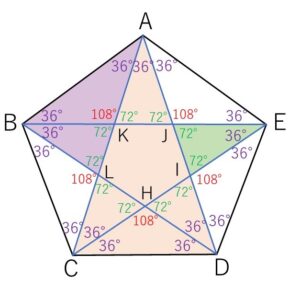
③1辺が正五角形の辺、2辺が対角線であるものは、\(△ACD\)をはじめ全部で5個でこれらは合同。
④1辺が正五角形の辺であるものはもう1種類あり、\(△ABL\)をはじめ全部で10個でこれらは合同(正五角形の1辺に対して2個ずつあるので全部で10個)。
⑤星型の図形の内部にも\(△EJI\)をはじめ全部で5個ありこれらは合同。
③と④と⑤の三角形は相似です。
(3)黄金比の登場
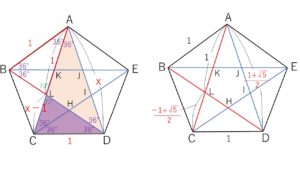
正五角形の一辺を\(1\)として対角線の長さを求めてみます。
\(△ABL\) は二等辺三角形だから、\(AL=1\)
\(△ACD ∽△DLC\) より 対角線の長さを\(x\)とすると
\(x:1=1:(x-1)\)
\(x^2-x-1=0\) を解いて
\(x=\displaystyle\frac{1+\sqrt{5}}{2}\) (\(>0\))
よって正五角形の辺と対角線の長さの比は
\(1:\displaystyle\frac{1+\sqrt{5}}{2}\)
となりますが、この比は黄金比とよばれている比です。
また、\(LC=x-1=\displaystyle\frac{-1+\sqrt{5}}{2}\) より
\(CL:LA\) についても
\(\displaystyle\frac{-1+\sqrt{5}}{2}:1=1:\displaystyle\frac{2}{-1+\sqrt{5}}=1:\displaystyle\frac{1+\sqrt{5}}{2}\)
と黄金比になっています。
同様に考えると、2本の対角線は互いに他方を黄金比になるように分けることが分かります。
(\(BL:LD\), \(AK:KC\), \(BK:KE\) など)
(4)平行線の登場
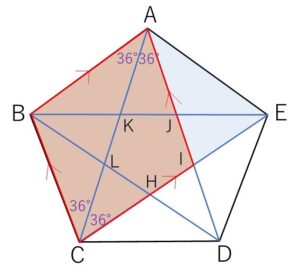
錯角が等しいことから、\(AB/\!/EC\) であり、同様に考えることにより正五角形の1つの辺に対して平行な対角線が1つ存在することになります。
よって四角形\(ABCE\) は \(BC=AE\) の等脚台形です。(同じ大きさの等脚台形は合計5個)
また、四角形\(ABCI\) については \(AB/\!/IC\) かつ \(BC/\!/AI\) より平行四辺形で、さらに \(AB=BC\) で隣り合う辺も等しいことから4辺が等しくなるので、ひし形となります。(同じ大きさのひし形は合計5個)
(\(AB,BC\)は正五角形の1辺、\(CI,IA\)も\(△CDI,△AIE\)が二等辺三角形であることから正五角形の1辺となるので、4辺が等しいと結論づけてもよいです)
(例題1)
1辺の長さが\(1\)の正五角形\(ABCDE\)がある。\(\vec{a}=\overrightarrow{AB}\), \(\vec{b}=\overrightarrow{AE}\), \(l=|\overrightarrow{EC}|\) とするとき、以下の問いに答えよ。
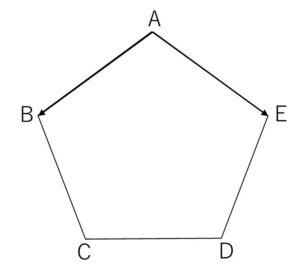
(1)\(AB\) と \(EC\) が平行であることに注意して、\(\overrightarrow{AC}\) を \(\vec{a},\vec{b},l\) を用いて表せ。
(2)内積 \(\vec{a}\cdot\vec{b}\) を \(l\) を用いて表せ。
(3)\(l\)を求めよ。
(4)\(\cos108°\) を求めよ。
(解答)
(1)
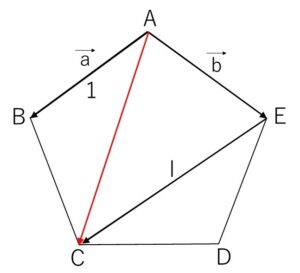
\(\overrightarrow{AC}=\overrightarrow{AE}+\overrightarrow{EC}\)
\(=\vec{b}+l\vec{a}\)
\(=l\vec{a}+\vec{b}\)
(2)
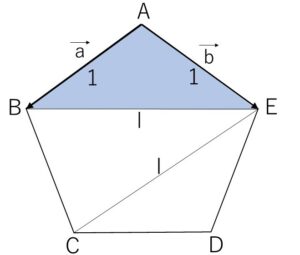
\(△ABE\) と \(△DEC\) について
2辺が大きさ\(1\)で、はさまれる角が正五角形の内角の1つで等しいので
\(△ABE≡△DEC\)
よって \(BE=EC=l\)
\(△ABE\)において余弦定理より
\(l^2=1^2+1^2-2|\vec{a}||\vec{b}|\cos BAE\)
\(l^2=2-2\vec{a}\cdot\vec{b}\)
したがって
\(\vec{a}\cdot\vec{b}=1-\displaystyle\frac{1}{2}l^2\)
(3)
同様に \(△BCA≡△DEC\) より \(CA=l\)
よって\(|\overrightarrow{AC}|^2=l^2\)
(1)より\(\overrightarrow{AC}=l\vec{a}+\vec{b}\) だから
\(|l\vec{a}+\vec{b}|^2=l^2\)
\(l^2|\vec{a}|^2+2l\vec{a}\cdot\vec{b}+|\vec{b}|^2=l^2\)
\(l^2+2l(1-\displaystyle\frac{1}{2}l^2)+1=l^2\)
\(l^3-2l-1=0\)
\((l+1)(l^2-l-1)=0\)
\(l=-1,\displaystyle\frac{1±\sqrt{5}}{2}\)
\(l>0\)より
\(l=\displaystyle\frac{1+\sqrt{5}}{2}\)
(4)
\(\cos \angle BAE=\displaystyle\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}\)
\(=\displaystyle\frac{1-\displaystyle\frac{1}{2}l^2}{1\cdot1}\)
\(=1-\displaystyle\frac{1}{2}\left(\displaystyle\frac{1+\sqrt
{5}}{2}\right)^2\)
\(=\displaystyle\frac{1-\sqrt{5}}{4}\)
正五角形の内角の和は\(540°\) だから
\(\angle BAE=540÷5=108°\)
よって
\(\cos108°=\displaystyle\frac{1-\sqrt{5}}{4}\)
(例題2)
1辺の長さが\(1\)の正五角形\(ABCDE\)に対し、\(\overrightarrow{AB}=\vec{a}\), \(\overrightarrow{BC}=\vec{b}\) とするとき、\(\overrightarrow{CD}\) を \(\vec{a},\vec{b}\) で表せ。
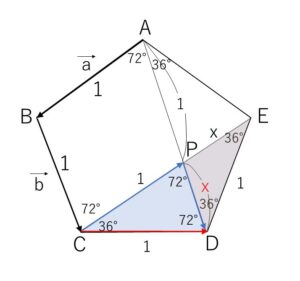
対角線 \(CE,AD\) をひき、交点を\(P\)とする。
図より同位角が等しいので \(AB/\!/CE\)
錯角が等しいので \(BC/\!/AD\)
よって、四角形\(ABCP\)は平行四辺形で \(AB=BC\) よりひし形。
ゆえに \(PD=x\) とおくと
\(\overrightarrow{CD}=\overrightarrow{CP}+\overrightarrow{PD}\)\(=-\vec{a}+x\vec{b}\)・・・①
今回は 108°,36°,36° の三角形の相似に着目して求めてみます。
ここで、\(△DEC∽△PDE\) より
\(DE:EC=PD:DE\)
\(1:(x+1)=x:1\)
\(x^2+x-1=0\)
\(x=\displaystyle\frac{-1±\sqrt{5}}{2}\)
\(x>0\) より
\(x=\displaystyle\frac{-1+\sqrt{5}}{2}\)
したがって①より
\(\overrightarrow{CD}=-\vec{a}+\displaystyle\frac{-1+\sqrt{5}}{2}\vec{b}\)
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→内積の図形的意味① back→内積と三角形の面積