引き続き内積の図形的意味に関する例題です。今回は円に関するものを扱っていきます。
(例題1)
円 \((x-2)^2+(y-2)^2=4\) の上を動く点\(P\)と、円 \((x+1)^2+(y+1)^2=1\) の上を動く点\(Q\)がある。このとき、内積 \(\overrightarrow{OP}\cdot\overrightarrow{OQ}\) の最大値と最小値を求めよ。ただし\(O\)は原点を表す。
(解答)
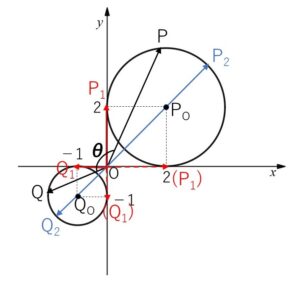
\(\overrightarrow{OP},\overrightarrow{OQ}\) のなす角を\(θ\)とすると
\(\overrightarrow{OP}\cdot\overrightarrow{OQ}=|\overrightarrow{OP}||\overrightarrow{OQ}|\cosθ\)
図より
\(90°≦θ≦180°\) だから
\(\overrightarrow{OP}\cdot\overrightarrow{OQ}≦0\)
よって最大値は \(θ=90°\) のとき \(\overrightarrow{OP}\cdot\overrightarrow{OQ}=0\)
(このとき\(P,Q\)は図の\(P_1,Q_1\))
最小値は \(|\overrightarrow{OP}|,|\overrightarrow{OQ}|\) が最大で \(θ=180°\) のときで
このとき \(P,Q\) は、図の \(P_2,Q_2\) となり・・・(注)
\(\overrightarrow{OP}\cdot\overrightarrow{OQ}\)
\(=OP_2×OQ_2×(-1)\)
\(=-(OP_O+P_OP_2)(OQ_O+Q_OQ_2)\)
\(=-(2\sqrt{2}+2)(\sqrt{2}+1)\)
\(=-6-4\sqrt{2}\)
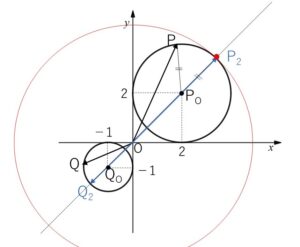
\(OP\)が最大となるときは、原点と円の中心 \(P_O(2,2)\) を結ぶ直線上に\(P\)があるときです(円と直線の交点は2個あるので\(O\)に近い方にも\(P\)がとれますが、このときは最小となります)。なぜならば、原点\(O\)を中心とする円を考えて半径をどんどん大きくしていくと、\(OP\)が最大となるときは、この原点中心の円に\(P_O(2,2)\)を中心とする円が内接するときの接点と\(P\)が一致するときであり、接点は2円の中心を結ぶ直線上にあるからです。
もしくは、三角不等式 \(OP≦OP_O+P_OP=OP_O+P_OP_2=2\sqrt{2}+2\) を考えてもよいです。
(例題2)
実数\(x,y,a,b\)が条件 \(x^2+y^2=1\) および \((a-2)^2+(b-2\sqrt{3})^2=1\) を満たすとき、\(ax+by\) の最大値、最小値を求めよ。
(解答)
座標平面で考える。
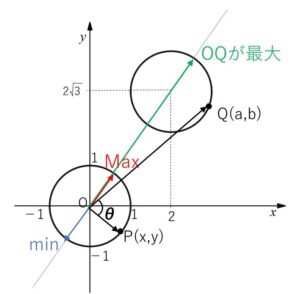
\(O(0,0)\)
\(x^2+y^2=1\) 上の点を \(P(x,y)\)
\((a-2)^2+(b-2\sqrt{3})^2=1\) 上の点を \(Q(a,b)\) とすると
\(ax+by=\overrightarrow{OP}\cdot\overrightarrow{OQ}=|\overrightarrow{OP}||\overrightarrow{OQ}|\cosθ=|\overrightarrow{OQ}|\cosθ\) (\(θ\)はベクトルのなす角)
よって最小値は \(OQ\) が最大で \(θ=180°\) のときであり、円の中心\((2,2\sqrt{3})\)と原点を通る直線の交点を考えると
\(ax+by=(\sqrt{2^2+(2\sqrt{3})^2}+1)×(-1)=-5\)
最大値は \(OQ\) が最大で \(θ=0°\) のときだから
\(ax+by=(\sqrt{2^2+(2\sqrt{3})^2}+1)×1=5\)
答 最小値\(-5\), 最大値\(5\)
最大値のとき \((a,b)=(\displaystyle\frac{5}{2},\displaystyle\frac{5\sqrt{3}}{2})\), \((x,y)=(\displaystyle\frac{1}{2},\displaystyle\frac{\sqrt{3}}{2})\)
最小値のとき \((a,b)=(\displaystyle\frac{5}{2},\displaystyle\frac{5\sqrt{3}}{2})\), \((x,y)=(-\displaystyle\frac{1}{2},-\displaystyle\frac{\sqrt{3}}{2})\)
(別解)
\(0°≦α,β<360°\)
\(x^2+y^2=1\) 上の点を \(P(\cosα,\sinα)\)
\((a-2)^2+(b-2\sqrt{3})^2=1\) 上の点を \(Q(2+\cosβ,2\sqrt{3}+\sinβ)\) とすると
\(ax+by\)
\(=\cosα(2+\cosβ)+\sinα(2\sqrt{3}+\sinβ)\)
\(=2(\sqrt{3}\sinα+\cosα)+(\cosα\cosβ+\sinα\sinβ)\)
\(=4\sin(α+30°)+\cos(α-β)\)
最大値は \(\sin(α+30°)=1\) かつ \(\cos(α-β)=1\) のとき \(4+1=\)\(5\)
このとき \(α+30°=90°\) かつ \(α-β=0°\)
つまり \(α=β=60°\)
最小値は \(\sin(α+30°)=-1\) かつ \(\cos(α-β)=-1\) のとき \(-4-1=\)\(-5\)
このとき \(α+30°=270°\) かつ \(α-β=-180°\) or \(180°\)
\(α=240°\) より \(α-β=-180°\) は不適だから
\(α=240°\), \(β=60°\)
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→分点・重心 back→内積の図形的意味①