内積の具体的な計算の演習です。
(例題1)
\(\angle A=120°\), \(\angle B=30°\), \(AC=\sqrt{3}\) の\(△ABC\)において、辺\(BC\)の中点を\(M\)とするとき、次の内積を求めよ。
(1)\(\overrightarrow{AB}\cdot\overrightarrow{AC}\)
(2)\(\overrightarrow{AM}\cdot\overrightarrow{BC}\)
(3)\(\overrightarrow{AC}\cdot\overrightarrow{CB}\)
(4)\((\overrightarrow{BC}-\overrightarrow{BA})\cdot\overrightarrow{CA}\)
本問では\(△ABC\)は二等辺三角形です。
(解答)
(1)
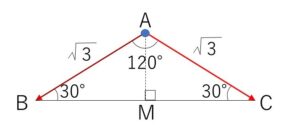
\(\overrightarrow{AB}\cdot\overrightarrow{AC}\)
\(=|\overrightarrow{AB}||\overrightarrow{AC}|\cos120°\)
\(=\sqrt{3}\cdot\sqrt{3}\cdot(-\displaystyle\frac{1}{2})\)
\(=-\displaystyle\frac{3}{2}\)
(2)
\(\overrightarrow{AM}\) と \(\overrightarrow{BC}\) は垂直だから
\(\overrightarrow{AM}\cdot\overrightarrow{BC}\)\(=0\)
(3)
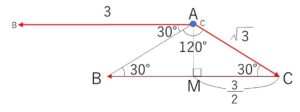
\(CM=\sqrt{3}\cos30°=\displaystyle\frac{3}{2}\) より
\(CB=3\)
(\(\overrightarrow{CB}\)の始点が\(A\)に重なるように平行移動するとなす角は\(150°\))
よって
\(\overrightarrow{AC}\cdot\overrightarrow{CB}\)
\(=|\overrightarrow{AC}||\overrightarrow{CB}|\cos150°\)
\(=\sqrt{3}\cdot3\cdot(-\displaystyle\frac{\sqrt{3}}{2})\)
\(=-\displaystyle\frac{9}{2}\)
(4)
((1)(3)を利用する方法だと)
\((\overrightarrow{BC}-\overrightarrow{BA})\cdot\overrightarrow{CA}\)
\(=\overrightarrow{BC}\cdot\overrightarrow{CA}-\overrightarrow{BA}\cdot\overrightarrow{CA}\)
\(=(-\overrightarrow{CB})\cdot(-\overrightarrow{AC})-(-\overrightarrow{AB})\cdot(-\overrightarrow{AC})\)
\(=\overrightarrow{AC}\cdot\overrightarrow{CB}-\overrightarrow{AB}\cdot\overrightarrow{AC}\)
\(=-\displaystyle\frac{9}{2}-(-\displaystyle\frac{3}{2})\)
\(=-3\)
(別解)
\((\overrightarrow{BC}-\overrightarrow{BA})\cdot\overrightarrow{CA}\)
\(=(\overrightarrow{AC})\cdot\overrightarrow{CA}\)
\(=-\overrightarrow{CA}\cdot\overrightarrow{CA}\)
\(=-|\overrightarrow{CA}|^2\)
\(=-3\)
(例題2)
3点 \(A(-1,3)\), \(B(1,-2)\), \(C(-4,-1)\) があるとき、内積 \(\overrightarrow{AB}\cdot\overrightarrow{CB}\) を求めよ。
(解答)
\(\overrightarrow{AB}=(1-(-1),-2-3)=(2,-5)\)
\(\overrightarrow{CB}=(1-(-4),-2-(-1))=(5,-1)\)
よって
\(\overrightarrow{AB}\cdot\overrightarrow{CB}\)
\(=2\cdot5+(-5)\cdot(-1)\)
\(=15\)
(例題3)
平面上で、ベクトル \(\overrightarrow{OA}\) と \(\overrightarrow{OB}\) は直交し、\(\overrightarrow{OA}=\overrightarrow{OB}=1\) を満たすとする。線分\(AB\)を3等分し、図のように\(A\)に近い点を\(P\)、\(B\)に近い点を\(Q\)とする。
\(\angle AOP=α\), \(\angle POQ=β\) とするとき、\(\cosα,\cosβ\) の値を求めよ。
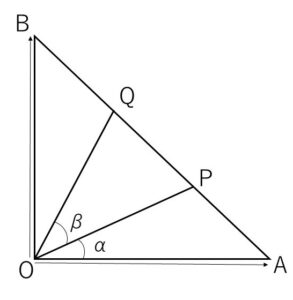
座標で考えて成分を求めていきます。
(解答)
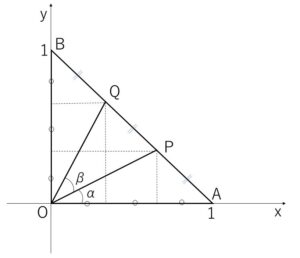
\(O(0,0)\), \(A(1,0)\), \(B(0,1)\) として座標平面で考える。
\(AB\)を3等分する点が\(P,Q\)なので、\(P,Q\)の座標は
\(P(\displaystyle\frac{2}{3},\displaystyle\frac{1}{3})\), \(Q(\displaystyle\frac{1}{3},\displaystyle\frac{2}{3})\)
よって
\(\overrightarrow{OA}\cdot\overrightarrow{OP}=|\overrightarrow{OA}||\overrightarrow{OP}|\cosα\) より
\(1\cdot\displaystyle\frac{2}{3}+0\cdot\displaystyle\frac{1}{3}=1\cdot\sqrt{(\displaystyle\frac{2}{3})^2+(\displaystyle\frac{1}{3})^2}\cosα\)
ゆえに
\(\cosα=\displaystyle\frac{2}{\sqrt{5}}\)
また
\(\overrightarrow{OP}\cdot\overrightarrow{OQ}=|\overrightarrow{OP}||\overrightarrow{OQ}|\cosβ\) より
\(\displaystyle\frac{2}{3}\cdot\displaystyle\frac{1}{3}+\displaystyle\frac{1}{3}\cdot\displaystyle\frac{2}{3}=\sqrt{(\displaystyle\frac{2}{3})^2+(\displaystyle\frac{1}{3})^2}\cdot\sqrt{(\displaystyle\frac{1}{3})^2+(\displaystyle\frac{2}{3})^2}\cosβ\)
ゆえに
\(\cosβ=\displaystyle\frac{4}{5}\)
(参考)三角関数を利用すればベクトルを用いずに計算できます。
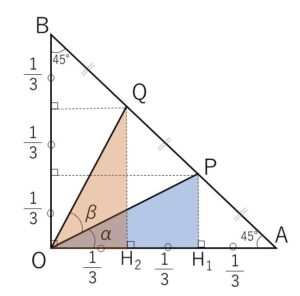
\(△OPH_1\) について
\(OP=\sqrt{(\displaystyle\frac{2}{3})^2+(\displaystyle\frac{1}{3})^2}\)\(=\displaystyle\frac{\sqrt{5}}{3}\)
よって
\(\cosα=\displaystyle\frac{OH_1}{OP}=\displaystyle\frac{\displaystyle\frac{2}{3}}{\displaystyle\frac{\sqrt{5}}{3}}\)\(=\displaystyle\frac{2}{\sqrt{5}}\)・・・①
\(\sinα=\displaystyle\frac{PH_1}{OP}=\displaystyle\frac{\displaystyle\frac{1}{3}}{\displaystyle\frac{\sqrt{5}}{3}}\)\(=\displaystyle\frac{1}{\sqrt{5}}\)・・・②
\(△OQH_2\) について
\(OQ=\sqrt{(\displaystyle\frac{1}{3})^2+(\displaystyle\frac{2}{3})^2}\)\(=\displaystyle\frac{\sqrt{5}}{3}\)
よって
\(\cos(α+β)=\displaystyle\frac{OH_2}{OQ}=\displaystyle\frac{1}{\sqrt{5}}\)
\(\sin(α+β)=\displaystyle\frac{QH_2}{OQ}=\displaystyle\frac{2}{\sqrt{5}}\)
加法定理より
\(\cosα\cosβ-\sinα\sinβ=\displaystyle\frac{1}{\sqrt{5}}\)
\(\sinα\cosβ+\cosα\sinβ=\displaystyle\frac{2}{\sqrt{5}}\)
①②を代入して
\(\displaystyle\frac{2}{\sqrt{5}}\cosβ-\displaystyle\frac{1}{\sqrt{5}}\sinβ=\displaystyle\frac{1}{\sqrt{5}}\)・・・③
\(\displaystyle\frac{1}{\sqrt{5}}\cosβ+\displaystyle\frac{2}{\sqrt{5}}\sinβ=\displaystyle\frac{2}{\sqrt{5}}\) ・・・④
③×2+④ より
\(\displaystyle\frac{5}{\sqrt{5}}\cosβ=\displaystyle\frac{4}{\sqrt{5}}\)
したがって
\(\cosβ=\displaystyle\frac{4}{5}\)
(さらに③に代入することで \(\sinβ=\displaystyle\frac{3}{5}\) も求まる)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→なす角 back→内積(成分表示)