対称(線対称)や回転に関する、ベクトルの問題について見ていきます。
(例題1)
平面上の三角形\(OAB\)は、\(\overrightarrow{OA}=\vec{a}\), \(\overrightarrow{OB}=\vec{b}\) とおくとき、\(|\vec{a}|=1\), \(|\vec{b}|=\sqrt{2}\), \(\vec{a}\cdot\vec{b}=\displaystyle\frac{1}{2}\) を満たすとする。辺\(AB\)を\(1:2\)に内分する点を\(P\)とし、直線\(OP\)に関して\(A\)と対称な点を\(Q\)、\(OQ\)の延長と\(AB\)の交点を\(R\)とおく。
(1)\(\overrightarrow{OQ}\)を\(\vec{a}\)と\(\vec{b}\)で表せ。
(2)\(\overrightarrow{OR}\)を\(\vec{a}\)と\(\vec{b}\)で表せ。
(3)\(△PQR\)の面積を求めよ。
\(\overrightarrow{OQ}=\overrightarrow{OA}+\)\(2\overrightarrow{AH}\)
です。\(\overrightarrow{AH}\)は垂直条件から求めます。
このように線対称については、対称な2点の線分\(AQ\)と軸\(OP\)の交点\(H\)について考えることが基本となります。
(解答)
(1)
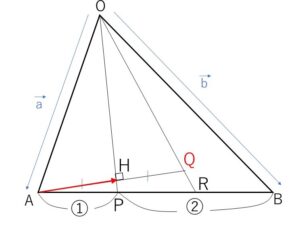
\(AQ\)と\(OP\)の交点を\(H\)とする。
\(\overrightarrow{OP}=\displaystyle\frac{2\vec{a}+\vec{b}}{1+2}\) より
\(\overrightarrow{OH}=k\overrightarrow{OP}=\displaystyle\frac{2}{3}k\vec{a}+\displaystyle\frac{1}{3}k\vec{b}\) とおける。
よって
\(\overrightarrow{AH}=\overrightarrow{OH}-\overrightarrow{OA}\)
\(=(\displaystyle\frac{2}{3}k-1)\vec{a}+\displaystyle\frac{1}{3}k\vec{b}\)・・・①
\(AH \perp OP\) だから
\(\{(\displaystyle\frac{2}{3}k-1)\vec{a}+\displaystyle\frac{1}{3}k\vec{b}\}\cdot(2\vec{a}+\vec{b})\cdot\displaystyle\frac{1}{3}=0\)
両辺\(9\)倍して
\(\{(2k-3)\vec{a}+k\vec{b}\}\cdot(2\vec{a}+\vec{b})=0\)
(\(|\vec{a}|^2=1\), \(|\vec{b}|^2=2\), \(\vec{a}\cdot\vec{b}=\displaystyle\frac{1}{2}\) より)
\((4k-6)+\displaystyle\frac{1}{2}(2k-3)+k+2k=0\)
よって
\(k=\displaystyle\frac{15}{16}\)
①より
\(\overrightarrow{AH}=(\displaystyle\frac{2}{3}k-1)\vec{a}+\displaystyle\frac{1}{3}k\vec{b}\)
\(=-\displaystyle\frac{3}{8}\vec{a}+\displaystyle\frac{5}{16}\vec{b}\)
となるので
\(\overrightarrow{OQ}=\overrightarrow{OA}+2\overrightarrow{AH}\)
\(=\vec{a}+2(-\displaystyle\frac{3}{8}\vec{a}+\displaystyle\frac{5}{16}\vec{b})\)
\(=\displaystyle\frac{1}{4}\vec{a}+\displaystyle\frac{5}{8}\vec{b}\)
(1)
\(\overrightarrow{OR}=s\overrightarrow{OQ}\)
\(=\displaystyle\frac{1}{4}s\vec{a}+\displaystyle\frac{5}{8}s\vec{b}\)・・・②
\(R\)は\(AB\)上にあるので
\(\displaystyle\frac{1}{4}s+\displaystyle\frac{5}{8}s=1\)
よって
\(s=\displaystyle\frac{8}{7}\)
したがって②より
\(\overrightarrow{OR}\)
\(=\displaystyle\frac{1}{4}s\vec{a}+\displaystyle\frac{5}{8}s\vec{b}\)
\(=\displaystyle\frac{2}{7}\vec{a}+\displaystyle\frac{5}{7}\vec{b}\)
(3)
他には(2)より \(AR:RB=5:2\) と分かるので、\(AP:PR\)も分かり、これらから全体\(△OAB\)と\(△PQR\)の比を求める方法もあります。
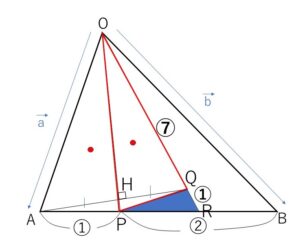
(2)より
\(\overrightarrow{OR}=\displaystyle\frac{8}{7}\overrightarrow{OQ}\) だから
\(OQ:QR=7:1\)
よって
\(△PQR=\displaystyle\frac{1}{7}△OQP\)
\(△OQP≡△OAP\) だから
\(△PQR=\displaystyle\frac{1}{7}△OAP\)・・・③
また、\(AP:PB=1:2\) より
\(△OAP=\displaystyle\frac{1}{3}△OAB\)・・・④
③④より
\(△PQR=\displaystyle\frac{1}{7}\cdot\displaystyle\frac{1}{3}△OAB\)
\(=\displaystyle\frac{1}{21}△OAB\)
ここで
\(△OAB=\displaystyle\frac{1}{2}\sqrt{|\vec{a}|^2|\vec{b}|^2-(\vec{a}\cdot\vec{b})^2}\)
\(=\displaystyle\frac{1}{2}\sqrt{1\cdot2-(\displaystyle\frac{1}{2})^2}\)
\(=\displaystyle\frac{\sqrt{7}}{4}\)
したがって
\(△PQR=\displaystyle\frac{1}{21}\cdot\displaystyle\frac{\sqrt{7}}{4}\)
\(=\displaystyle\frac{\sqrt{7}}{84}\)
(例題2)
座標平面上で、始点が原点であるベクトル \(\vec{a}=(\displaystyle\frac{2}{\sqrt{5}},\displaystyle\frac{1}{\sqrt{5}})\)を、原点を中心として反時計回りに\(90°\)回転したベクトルを\(\vec{b}\)とする。
このとき、ベクトル \((\displaystyle\frac{7}{\sqrt{5}},-\displaystyle\frac{4}{\sqrt{5}})\) を \(s\vec{a}+t\vec{b}\) の形に表せ。
三角関数を利用するか、図で考えるか、複素数の回転(数Ⅲ)を利用することになりますが、解答では三角関数を利用したいと思います。
(解答)
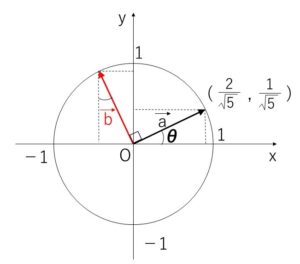
\(\vec{a}\)が\(x\)軸の正の方向となす角を\(θ\)とおくと、\(|\vec{a}|=1\) より
\(\cosθ=\displaystyle\frac{2}{\sqrt{5}}\), \(\sinθ=\displaystyle\frac{1}{\sqrt{5}}\)
よって
\(\vec{b}=(\cos(θ+90°),\sin(θ+90°))\)
\(=(-\sinθ,\cosθ)\)
\(=(-\displaystyle\frac{1}{\sqrt{5}},\displaystyle\frac{2}{\sqrt{5}})\)
\(s\vec{a}+t\vec{b}\)
\(=s(\displaystyle\frac{2}{\sqrt{5}},\displaystyle\frac{1}{\sqrt{5}})+t(-\displaystyle\frac{1}{\sqrt{5}},\displaystyle\frac{2}{\sqrt{5}})\)
\(=(\displaystyle\frac{2s-t}{\sqrt{5}},\displaystyle\frac{s+2t}{\sqrt{5}})\)
これが \((\displaystyle\frac{7}{\sqrt{5}},-\displaystyle\frac{4}{\sqrt{5}})\) と等しいから
\(2s-t=7\), \(s+2t=-4\)
\(s,t\)について解いて
\(s=2\), \(t=-3\)
したがって
\((\displaystyle\frac{7}{\sqrt{5}},-\displaystyle\frac{4}{\sqrt{5}})=2\vec{a}-3\vec{b}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→座標とベクトル back→点の一致