座標とベクトル

条件を満たす座標をベクトルを用いて求める問題について見ていきます。

(例題1)
2点 \(S(s,s)\), \(T(-t,t)\) \([s≧0, t≧0]\) について、\(s^2+t^2=2\) とし、点\(P(x,y)\)  \([|x|≦y]\) を\(△SPT\)が正三角形になるようにする。また、\(M\)を線分\(ST\)の中点とし、\(O\)を原点とする。直線\(PM\)と\(x\)軸との交点を\(R\)とする。

(1)\(ST=2\), \(OM=1\), \(MR=1\) であることを示せ。
(2)\(\overrightarrow{OM}\) が\(x\)軸の正の方向となす角を\(θ\)とするとき、\(P\)の座標 \((x,y)\) を\(θ\)を用いて表せ。

(解答)
(1)

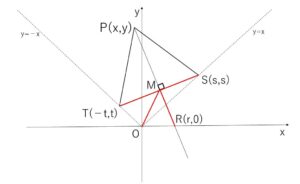
\(ST=\sqrt{(s+t)^2+(s-t)^2}\)
\(=\sqrt{2(s^2+t^2)}\)
\(=2\)

\(M(\displaystyle\frac{s-t}{2},\displaystyle\frac{s+t}{2})\) だから

\(OM=\sqrt{(\displaystyle\frac{s-t}{2})^2+(\displaystyle\frac{s+t}{2})^2}\)
\(=\sqrt{\displaystyle\frac{s^2+t^2}{2}}\)
\(=1\)

\(R(r,0)\) とすると、\(\overrightarrow{TS} \perp \overrightarrow{MR}\) より

\((s+t,s-t)\cdot(r-\displaystyle\frac{s-t}{2},-\displaystyle\frac{s+t}{2})=0\)
\((s+t)(r-\displaystyle\frac{s-t}{2})+(s-t)(-\displaystyle\frac{s+t}{2})=0\)
\((s+t)\{(r-\displaystyle\frac{s-t}{2})-\displaystyle\frac{s-t}{2}\}=0\)
\((s+t)(r-s+t)=0\)・・・①

ここで、\(s^2+t^2=2\) より \((s,t)≠(0,0)\) だから
\(s+t>0\) となるので①より
\(r=s-t\)

したがって
\(MR=\sqrt{\{\displaystyle\frac{s-t}{2}-(s-t)\}^2+(\displaystyle\frac{s+t}{2})^2}\)
\(=\sqrt{(-\displaystyle\frac{s-t}{2})^2+(\displaystyle\frac{s+t}{2})^2}\)
\(=1\)

(2)

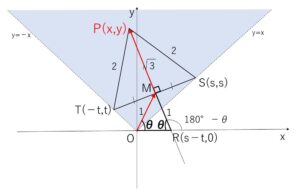
\(OM=MR=1\) より　\(\angle MRO=θ\)

よって
\(\overrightarrow{OM}=(\cosθ,\sinθ)\)
\(\overrightarrow{RM}=(\cos(180°-θ),\sin(180°-θ))\)\(=(-\cosθ,\sinθ)\)

\(ST=2\)より正三角形の1辺の大きさは\(2\)だから
\(MP=\sqrt{3}\)

ゆえに
\(\overrightarrow{OP}\)
\(=\overrightarrow{OM}+\overrightarrow{MP}\)
\(=\overrightarrow{OM}+\sqrt{3}\overrightarrow{RM}\)
\(=(\cosθ-\sqrt{3}\cosθ,\sinθ+\sqrt{3}\sinθ)\)

したがって
\(P(\cosθ-\sqrt{3}\cosθ,\sinθ+\sqrt{3}\sinθ)\)

(注)

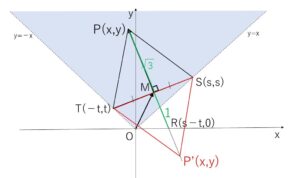
正三角形はもう1つ作ることができますが、
\(MP=\sqrt{3}\), \(MR=1\) より
\(y=±x\) (\(y≧0\)) の下側に\(P’\)がきてしまうので、\(|x|≦y\) を満たしません。

(例題2)
平面の原点\(O\)を端点とし、\(x\)軸となす角がそれぞれ \(-α,α\)　(ただし\(0<α<60°\)) である半直線を\(L_1,L_2\)とする。\(L_1\)上に点\(P\)、\(L_2\)上に点\(Q\)を線分\(PQ\)の長さが\(1\)となるようにとり、点\(R\)を、直線\(PQ\)に対し原点\(O\)の反対側に\(△PQR\)が正三角形になるようにとる。\(\overrightarrow{PQ}\) が \(x\)軸の正の方向となす角を\(θ\)　(ただし \(α<θ<180°-α\))　とするとき、点\(R\)の座標を\(α,θ\)を用いて表せ。

(解答)

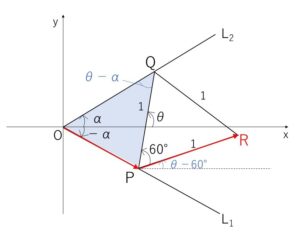
\(△OPQ\)において正弦定理より
\(\displaystyle\frac{OP}{\sin(θ-α)}=\displaystyle\frac{1}{\sin2α}\)

\(∴OP=\displaystyle\frac{\sin(θ-α)}{\sin2α}\)

よって
\(\overrightarrow{OP}=(OP\cos(-α),OP\sin(-α))\)

\(=(\displaystyle\frac{\cosα\sin(θ-α)}{2\sinα\cosα},\displaystyle\frac{-\sinα\sin(θ-α)}{2\sinα\cosα})\)

\(=(\displaystyle\frac{\sin(θ-α)}{2\sinα},\displaystyle\frac{-\sin(θ-α)}{2\cosα})\)

ゆえに
\(\overrightarrow{OR}=\overrightarrow{OP}+\overrightarrow{PR}\)

\(=(\displaystyle\frac{\sin(θ-α)}{2\sinα},\displaystyle\frac{-\sin(θ-α)}{2\cosα})+(\cos(θ-60°),\sin(θ-60°))\)

\(=(\displaystyle\frac{\sin(θ-α)}{2\sinα}+\cos(θ-60°),\displaystyle\frac{-\sin(θ-α)}{2\cosα}+\sin(θ-60°))\)

\(x\)成分について
\(\displaystyle\frac{\sin(θ-α)}{2\sinα}+\cos(θ-60°)\)

\(=\displaystyle\frac{\sinθ\cosα-\cosθ\sinα+2\sinα(\cosθ\cdot\displaystyle\frac{1}{2}+\sinθ\cdot\displaystyle\frac{\sqrt{3}}{2})}{2\sinα}\)

\(=\displaystyle\frac{\cosα+\sqrt{3}\sinα}{2\sinα}\sinθ\)

\(=\displaystyle\frac{\cosα\cos60°+\sinα\sin60°}{\sinα}\sinθ\)

\(=\displaystyle\frac{\cos(α-60°)}{\sinα}\sinθ\)

\(y\)成分について
\(\displaystyle\frac{-\sin(θ-α)}{2\cosα}+\sin(θ-60°)\)

\(=\displaystyle\frac{-(\sinθ\cosα-\cosθ\sinα)+2\cosα(\sinθ\cdot\displaystyle\frac{1}{2}-\cosθ\cdot\displaystyle\frac{\sqrt{3}}{2})}{2\cosα}\)

\(=\displaystyle\frac{\sinα-\sqrt{3}\cosα}{2\cosα}\cosθ\)

\(=\displaystyle\frac{\sin(α-60°)}{\cosα}\cosθ\)

したがって
\(R(\displaystyle\frac{\cos(α-60°)}{\sinα}\sinθ,\displaystyle\frac{\sin(α-60°)}{\cosα}\cosθ)\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→直線の方程式　back→対称・回転とベクトル