点Pの位置ベクトル | 教えて数学理科

点\(P\)に関するベクトルの等式が与えられた場合の、点\(P\)の位置に関する例題です。

(例題1)
\(△ABC\)と、\(\overrightarrow{PA}+3\overrightarrow{PB}+4\overrightarrow{PC}=\vec{0}\) を満たす\(△ABC\)の内部の点\(P\)がある。

(1)点\(P\)はどのような位置にあるか。
(2)\(△PBC\), \(△PCA\), \(△PAB\) の面積をそれぞれ、\(S_1,S_2,S_3\) とするとき、\(S_1:S_2:S_3\) を求めよ。

\(△ABC\)と\(P\)の位置関係を知りたいので、3点\(A,B,C\)のうちどれかを基準にとることになります。例えば\(A\)を基準にすると、2つのベクトル \(\overrightarrow{AB},\overrightarrow{AC}\) は平行でなく、\(\vec{0}\)でもないので1次独立。よってこの2つのベクトルで任意の点を表すことができます(もちろん\(P\)についても表せる)。
したがって与えられた等式を\(A\)を始点とするベクトルに変形すればよいです。
最終目標は \(\overrightarrow{AP}=(\overrightarrow{AB},\overrightarrow{AC}の式)\) という形です。

(解答)
(1)
\(\overrightarrow{PA}+3\overrightarrow{PB}+4\overrightarrow{PC}=\vec{0}\) より

\(-\overrightarrow{AP}+3(\overrightarrow{AB}-\overrightarrow{AP})+4(\overrightarrow{AC}-\overrightarrow{AP})=\vec{0}\)

\(\overrightarrow{AP}=\displaystyle\frac{3\overrightarrow{AB}+4\overrightarrow{AC}}{8}\)

ここからの式変形は少し工夫が必要です。
右辺の分子 \(3\overrightarrow{AB}+4\overrightarrow{AC}\) と内分点の公式を意識すると、分母に\(7\)があると都合がよいので、無理やり\(7\)に変えます。あとはもとの値と同じになるように調整します。

\(\overrightarrow{AP}=\displaystyle\frac{3\overrightarrow{AB}+4\overrightarrow{AC}}{7}×\displaystyle\frac{7}{8}\)

\(\overrightarrow{AD}=\displaystyle\frac{3\overrightarrow{AB}+4\overrightarrow{AC}}{4+3}\) とおくと

点\(D\)は線分\(BC\)を\(4:3\)に内分する点となり

\(\overrightarrow{AP}=\displaystyle\frac{7}{8}\overrightarrow{AD}\)

より、点\(P\)は線分\(AD\)を\(7:1\)に内分する点。

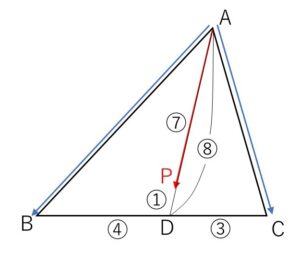
P位置ベクトル例題1-1

以上より点\(P\)は、線分\(BC\)を\(4:3\)に内分する点を\(D\)とすると、線分\(AD\)を\(7:1\)に内分する点である。

(2)

\(△ABC\)の面積を\(S\)とおけば、(1)で求めた比より各三角形の面積を\(S\)で表すことができます。

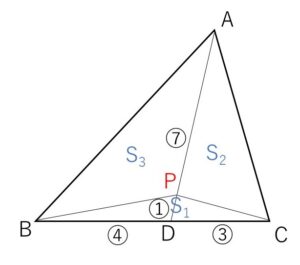
P位置ベクトル例題1-2

\(△ABC\)の面積を\(S\)とおくと

\(S_1=\displaystyle\frac{4}{7}\cdot\displaystyle\frac{1}{8}S+\displaystyle\frac{3}{7}\cdot\displaystyle\frac{1}{8}S=\displaystyle\frac{1}{8}S\)

\(S_2=\displaystyle\frac{3}{7}\cdot\displaystyle\frac{7}{8}S=\displaystyle\frac{3}{8}S\)

\(S_3=\displaystyle\frac{4}{7}\cdot\displaystyle\frac{7}{8}S=\displaystyle\frac{4}{8}S\)

よって
\(S_1:S_2:S_3=1:3:4\)

(例題2)
\(l,m,n\)を正の数とする。\(△ABC\)に対して
\(l\overrightarrow{PA}+m\overrightarrow{PB}+n\overrightarrow{PC}=\vec{0}\) を満たす点\(P\)は、\(△ABC\)の内部にあることを示せ。

係数が文字ですが、やることは(例題1)と変わりません。

(解答)
\(l\overrightarrow{PA}+m\overrightarrow{PB}+n\overrightarrow{PC}=\vec{0}\) より

\(-l\overrightarrow{AP}+m(\overrightarrow{AB}-\overrightarrow{AP})+n(\overrightarrow{AC}-\overrightarrow{AP})=\vec{0}\)

\(\overrightarrow{AP}=\displaystyle\frac{m\overrightarrow{AB}+n\overrightarrow{AC}}{l+m+n}\)

よって
\(\overrightarrow{AP}=\displaystyle\frac{m\overrightarrow{AB}+n\overrightarrow{AC}}{n+m}\cdot\displaystyle\frac{m+n}{l+m+n}\)

ここで
\(\overrightarrow{AD}=\displaystyle\frac{m\overrightarrow{AB}+n\overrightarrow{AC}}{n+m}\)　とおくと、点\(D\)は線分\(BC\)を \(n:m\) に内分する点であり

\(\overrightarrow{AP}=\displaystyle\frac{m+n}{l+m+n}\overrightarrow{AD}\) より、点\(P\)は線分\(AD\)を \((m+n):l\) に内分する点である。

したがって点\(P\)は\(△ABC\)の内部にある。

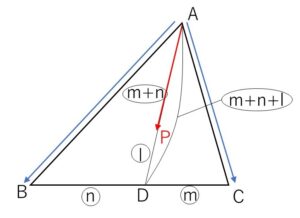
P位置ベクトル例題2

内分する点なので、\(D\)は\(B,C\)を除く線分\(BC\)上にあり、\(P\)は\(A,D\)を除く線分\(AD\)上にあることから、\(P\)は\(△ABC\)の内部にあります(\(△ABC\)の辺上にはない)。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→交点の位置ベクトル①　back→分点・重心