直線や円などの図形をベクトルを用いて表す方法について見ていきます。
まずは直線からです。
・直線のベクトル方程式 (方向ベクトルによる表記)
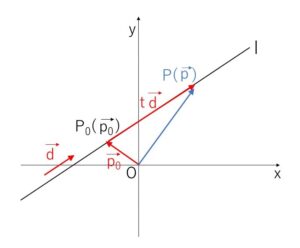
定点\(P_0(\vec{p_0})\)を通り、\(\vec{0}\)でないベクトル\(\vec{d}\)に平行な直線を\(l\)とします。
この直線上\(l\)の点を\(P(\vec{p})\)とすると、\(\overrightarrow{P_0P}/\!/\vec{d}\) または \(\overrightarrow{P_0P}=\vec{0}\) だから
\(\overrightarrow{P_0P}=t\vec{d}\) (\(t\)は実数)
よって
\(\vec{p}-\vec{p_0}=t\vec{d}\)
\(\vec{p}=\vec{p_0}+t\vec{d}\)・・・① (方向ベクトルによる直線の方程式)
①において、\(t\)がすべての実数値をとって変化すると点\(P(\vec{p})\)は直線\(l\)上のすべての点を動くので①が直線\(l\)を表していることになります。そこで①を直線\(l\)のベクトル方程式とよびます。また直線\(l\)の方向を決める\(\vec{d}\)のようなベクトルを方向ベクトルとよびます。
ここでベクトル方程式①を成分表示にしてみます。
\(P(x,y)\), \(P_0(x_0,y_0)\), \(\vec{d}=(a,b)\) とすると
\(\vec{p}=(x,y)\), \(\vec{p_0}=(x_0,y_0)\) となるので①より
\((x,y)=(x_0,y_0)+t(a,b)\)
よって
\(x=x_0+at\)・・・②
\(y=y_0+bt\)・・・③
そして②③を直線\(l\)の媒介変数表示、\(t\)を媒介変数とよびます。
また \(a≠0\) のとき②より
\(t=\displaystyle\frac{x-x_0}{a}\)
これを③に代入すると
\(y=\displaystyle\frac{b}{a}(x-x_0)+y_0\)・・・④
と見慣れた直線の方程式になります。
・直線のベクトル方程式 (2点を通る直線)
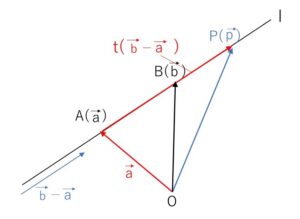
2点\(A(\vec{a}),B(\vec{b})\)を通る直線を\(l\)とすると
直線\(l\)は、「\(A(\vec{a})\) を通る 方向ベクトル\(\vec{b}-\vec{a}\) の直線」なので、直線上の点を\(P(\vec{p})\)とすると、直線\(l\)のベクトル方程式は
\(\vec{p}=\vec{a}+t(\vec{b}-\vec{a})\)・・・(i)
よって
\(\vec{p}=(1-t)\vec{a}+t\vec{b}\)・・・(ii)
ここで(ii)の右辺の係数の和が\(1\)になることに着目して、\(1-t=s\) とおくと次のように表すこともできます。
\(\vec{p}=s\vec{a}+t\vec{b}\), \(s+t=1\)
また \(A(a_1,a_2)\), \(B(b_1,b_2)\), \(P(x,y)\) とおくと(i)より
\((x,y)=(a_1,a_2)+t(b_1-a_1,b_2-a_2)\)
成分を比較して
\(x=a_1+t(b_1-a_1)\)・・・(iii)
\(y=a_2+t(b_2-a_2)\)・・・(iv)
(iii)より \(a_1≠b_1\) のとき
\(t=\displaystyle\frac{x-a_1}{b_1-a_1}\)
これを(iv)に代入すると
\(y=\displaystyle\frac{b_2-a_2}{b_1-a_1}(x-a_1)+a_2\)
と見慣れた2点を通る直線の方程式となります。
(例題)
(1)\(A(\vec{a}),B(\vec{b}),C(\vec{c})\) とする。\(M\)を辺\(BC\)の中点とするとき、直線\(AM\) (中線) のベクトル方程式を求めよ。
(2)定三角形\(ABC\)と平面\(ABC\)上の定点\(O\)について
\(x\overrightarrow{OA}+y\overrightarrow{OB}+\displaystyle\frac{1}{2}\overrightarrow{OC}=\overrightarrow{OQ}\) (ただし \(x+y=\displaystyle\frac{1}{2}\) とする)
を満足する点\(Q\)はどのような図形上にあるか。
(解答)
(1)
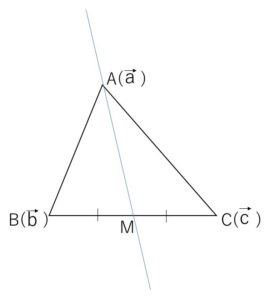
\(M(\vec{m})\)とおくと、\(\vec{m}=\displaystyle\frac{\vec{b}+\vec{c}}{2}\) より、\(AM\)の方向ベクトルは
\(\displaystyle\frac{\vec{b}+\vec{c}}{2}-\vec{a}\)
よって\(AM\)のベクトル方程式は直線上の点を\(P(\vec{p})\)とすると
\(\vec{p}=\vec{a}+t(\displaystyle\frac{\vec{b}+\vec{c}}{2}-\vec{a})\) (\(t\)は実数)
(2)
\(x\overrightarrow{OA}+y\overrightarrow{OB}+\displaystyle\frac{1}{2}\overrightarrow{OC}=\overrightarrow{OQ}\)・・・①
\(y=\displaystyle\frac{1}{2}-x\)を①に代入して
(\(Q\)の位置が知りたいので \(\overrightarrow{OQ}=\cdots\) の形にします)
\(\overrightarrow{OQ}=x\overrightarrow{OA}+(\displaystyle\frac{1}{2}-x)\overrightarrow{OB}+\displaystyle\frac{1}{2}\overrightarrow{OC}\)
(\(x\)とそれ以外でまとめると)
\(\overrightarrow{OQ}=\displaystyle\frac{1}{2}\overrightarrow{OB}+\displaystyle\frac{1}{2}\overrightarrow{OC}+x(\overrightarrow{OA}-\overrightarrow{OB})\)
\(=\displaystyle\frac{\overrightarrow{OB}+\overrightarrow{OC}}{2}+x\overrightarrow{BA}\)
したがって、点\(Q\)は辺\(BC\)の中点を通り\(BA\)に平行な直線上にある。
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→円の方程式 back→座標とベクトル