交点のベクトル表示を求める問題などは、チェバの定理、メネラウスの定理を用いて解くことができる場合があります。まずはこれらの定理についておさらいしておきます。(証明は省略します)
・チェバの定理
\(△ABC\)の3頂点\(A,B,C\)と、三角形の辺上またはその延長上にない点\(O\)とを結んで3直線をひく。3直線\(AO,BO,CO\)が対辺\(BC,CA,AB\)またはその延長と交わるとき、交点をそれぞれ\(P,Q,R\)とすると
\(\displaystyle\frac{BP}{PC}\cdot\displaystyle\frac{CQ}{QA}\cdot\displaystyle\frac{AR}{RB}=1\)
とくに\(O\)を\(△ABC\)の内部にとると次のような図になります。
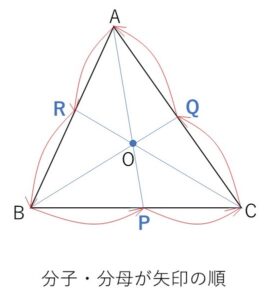
・メネラウスの定理
\(△ABC\)の辺\(BC,CA,AB\)またはその延長が、三角形の頂点を通らない1直線とそれぞれ点\(P,Q,R\)で交わるとき
\(\displaystyle\frac{BP}{PC}\cdot\displaystyle\frac{CQ}{QA}\cdot\displaystyle\frac{AR}{RB}=1\)
とくに1直線が辺と交わるときは次のような図になります。
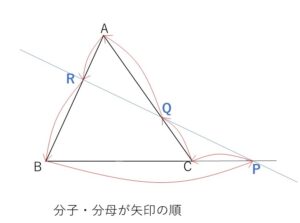
分子と分母は、どちらも頂点から\(P,Q,R\)までの長さを考えます。
(例題)
\(△OAB\)において、辺\(OA\)を \(s:(1-s)\) の比に内分する点を\(P\)、辺\(OB\)を \(t:(1-t)\) の比に内分する点を\(Q\)とする。また、\(BP\)と\(AQ\)との交点を\(R\)、\(OR\)の延長と辺\(AB\)の交点を\(S\)とする。\(\overrightarrow{OA}=\vec{a}\), \(\overrightarrow{OB}=\vec{b}\), \(0<s<1\), \(0<t<1\) とするとき
(1)\(\overrightarrow{OR}\) を \(\vec{a},\vec{b},s,t\) で表せ。
(2)\(\overrightarrow{OS}\) を \(\vec{a},\vec{b},s,t\) で表せ。
もちろん、係数比較 や 係数の和=1 などを用いても解けますが、せっかくなのでチェバの定理、メネラウスの定理を用いて解いていきます。
(2)については、チェバの定理から \(AS:SB\) が分かります。
(1)については、順番は前後しますがこの\(AS:SB\)を使ってメネラウスの定理より\(OR:RS\) を求めたり、順番通りにやるなら同じくメネラウスの定理を使って(三角形と直線は変わる)\(AR:RQ\)や\(PR:RB\)などを求める方法もあります。
(解答)
(1)(2)
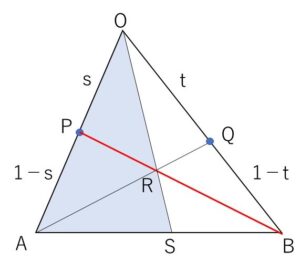
チェバの定理より
\(\displaystyle\frac{AS}{SB}\cdot\displaystyle\frac{1-t}{t}\cdot\displaystyle\frac{s}{1-s}=1\)
\(\displaystyle\frac{AS}{SB}=\displaystyle\frac{t(1-s)}{s(1-t)}\)
よって
\(AS:SB=t(1-s):s(1-t)\)・・・①
また
\(△OAS\)と直線\(PB\)についてメネラウスの定理から、①より
\(\displaystyle\frac{s+t-2st}{s(1-t)}\cdot\displaystyle\frac{SR}{RO}\cdot\displaystyle\frac{s}{1-s}=1\)
\(\displaystyle\frac{SR}{RO}=\displaystyle\frac{(1-s)(1-t)}{s+t-2st}\)
よって
\(SR:RO=(1-s)(1-t):(s+t-2st)\)・・・②
①より \(t(1-s)+s(1-t)=s+t-2st\) だから
\(\overrightarrow{OS}=\displaystyle\frac{s(1-t)\vec{a}+t(1-s)\vec{b}}{s+t-2st}\)
\(=\displaystyle\frac{s(1-t)}{s+t-2st}\vec{a}+\displaystyle\frac{t(1-s)}{s+t-2st}\vec{b}\)
また②より \((1-s)(1-t)+(s+t-2st)=1-st\) だから
\(\overrightarrow{OR}=\displaystyle\frac{s+t-2st}{1-st}\overrightarrow{OS}\)
\(=\displaystyle\frac{s(1-t)}{1-st}\vec{a}+\displaystyle\frac{t(1-s)}{1-st}\vec{b}\)
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→1次従属なベクトルと対称性 back→三角形の形状