円の方程式

円のベクトル方程式について見ていきます。

・円のベクトル方程式(中心\(C\),半径\(r\))

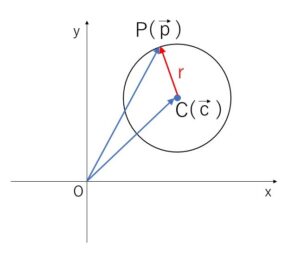
点\(C(\vec{c})\)を中心とする半径\(r\)の円は、円周上の点を\(P(\vec{p})\)とすると

\(|\overrightarrow{CP}|=r\)
よって
\(|\vec{p}-\vec{c}|=r\)・・・①　(中心\(C\),半径\(r\)の円のベクトル方程式)

また①の両辺を2乗することで、次のような形で表すこともできます。
\((\vec{p}-\vec{c})\cdot(\vec{p}-\vec{c})=r^2\)・・・②

ここで座標平面における原点を基準として \(\vec{p}=(x,y)\), \(\vec{c}=(a,b)\) と成分表示すると、②より

\((x-a,y-b)\cdot(x-a,y-b)=r^2\)  となるので

\((x-a)^2+(y-b)^2=r^2\)

と見慣れた円の方程式になります。

・円のベクトル方程式(線分\(AB\)が直径)
\(A(\vec{a})\), \(B(\vec{b})\) を結ぶ線分\(AB\)を直径とする円のベクトル方程式を考えていきます。

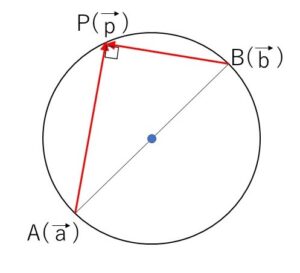
円周の半分の弧に対する円周角は\(90°\)であることに注意すると、点\(P(\vec{p})\)が円周上にある条件(必要十分条件)は

「\(AP \perp BP\) または \(P\)が\(A\)または\(B\)に一致」

よって
「\(\overrightarrow{AP} \perp \overrightarrow{BP}\) または \(\overrightarrow{AP}=\vec{0}\) または \(\overrightarrow{BP}=\vec{0}\)」

ゆえに
「\(\overrightarrow{AP}\cdot\overrightarrow{BP}=0\)」

したがってこの円のベクトル方程式は次のように表されます。
\((\vec{p}-\vec{a})\cdot(\vec{p}-\vec{b})=0\)・・・(i)　(\(AB\)を直径とする円のベクトル方程式)

もしくは、
中心が線分\(AB\)の中点、半径が線分\(AB\)の長さの半分の円と考えると

\(|\vec{p}-\displaystyle\frac{\vec{a}+\vec{b}}{2}|=\displaystyle\frac{|\vec{a}-\vec{b}|}{2}\)・・・(ii)

と表すこともできます。

ここで座標平面上の原点を基準として、
\(\vec{p}=(x,y)\),　\(\vec{a}=(a_1,a_2)\),　\(\vec{b}=(b_1,b_2)\)
と成分表示して、(i)または(ii)を式変形することで

\((x-\displaystyle\frac{a_1+b_1}{2})^2+(y-\displaystyle\frac{a_2+b_2}{2})^2=\left\{\displaystyle\frac{\sqrt{(a_1-b_1)^2+(a_2-b_2)^2}}{2}\right\}^2\)

(\(AB\)の中点を中心とする、半径が\(AB\)の長さの半分の円)

を導くことでができます。

(例題1)
3点 \(A(1,0)\), \(B(0,1)\), \(C(2,2)\) に対して、点\(P\)が
\(|\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}|=3\)
を満たしたながら動くとき、点\(P\)はどのような図形上を描くか。

(解答)
(解法1)ベクトルのまま変形
\(O(0,0)\) とする。

\(\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}\)
\(=(\overrightarrow{OA}-\overrightarrow{OP})+(\overrightarrow{OB}-\overrightarrow{OP})+(\overrightarrow{OC}-\overrightarrow{OP})\)
\(=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}-3\overrightarrow{OP}\) より

\(|\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}-3\overrightarrow{OP}|=3\)
両辺\(3\)で割ると
\(|\displaystyle\frac{\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}}{3}-\overrightarrow{OP}|=1\)・・・①

ここで
\(\displaystyle\frac{\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}}{3}=\overrightarrow{OG}\) とおくと (\(G\)は\(△ABC\)の重心になる)

\(\overrightarrow{OG}=(1,1)\)
また①は
\(|\overrightarrow{OG}-\overrightarrow{OP}|=1\)
\(|\overrightarrow{PG}|=1\)　(\(|\overrightarrow{GP}|=1\))

したがって点\(P\)は、\((1,1)\)を中心とする半径\(1\)の円周上を動く。

(解法2)成分表示
\(P(x,y)\)とすると
\(\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}\)
\(=(1-x,-y)+(-x,1-y)+(2-x,2-y)\)
\(=(3-3x,3-3y)\)

\(|\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}|^2=3^2\) より

\((3-3x)^2+(3-3y)^2=9\)
よって
\((x-1)^2+(y-1)^2=1\)
(\((1,1)\)を中心とする半径\(1\)の円)

(例題2)
平面上に原点\(O\)を中心とする半径\(1\)の円\(K_1\)を考える。\(K_1\)の直径を1つとり、その両端を\(A,B\)とする。円\(K_1\)の周上の任意の点\(Q\)に対し、線分\(QA\)を\(1:2\)の比に内分する点を\(R\)とする。いま、\(k\)を正の定数として
\(\vec{p}=\overrightarrow{AQ}+k\overrightarrow{BR}\)
とおく。ただし、\(Q=A\) のときは \(R=A\)とする。また、\(\overrightarrow{OA}=\vec{a}\), \(\overrightarrow{OQ}=\vec{q}\) とおく。

(1)\(\overrightarrow{BR}\)を\(\vec{a},\vec{q}\)を用いて表せ。
(2)点\(Q\)が円\(K_1\)の周上を動くとき、\(\overrightarrow{OP}=\vec{p}\) となるような点\(P\)が描く図形を\(K_2\)とする。\(K_2\)は円であることを示し、中心の位置ベクトルと半径を求めよ。
(3)円\(K_2\)の内部に点\(A\)が含まれるような\(k\)の値の範囲を求めよ。

(解答)
(1)

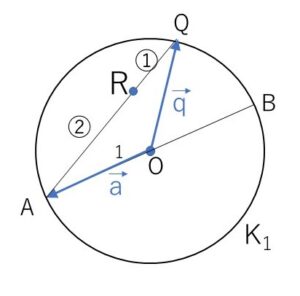
\(\overrightarrow{BR}\)
\(=\overrightarrow{OR}-\overrightarrow{OB}\)
\(=\displaystyle\frac{2\vec{q}+\vec{a}}{1+2}-(-\overrightarrow{OA})\)
\(=\displaystyle\frac{2\vec{q}+\vec{a}}{3}+\vec{a}\)
\(=\displaystyle\frac{4}{3}\vec{a}+\displaystyle\frac{2}{3}\vec{q}\)

(2)

\(\vec{p}=\overrightarrow{AQ}+k\overrightarrow{BR}\)　と(1)より

\(\vec{p}=(\vec{q}-\vec{a})+k(\displaystyle\frac{4}{3}\vec{a}+\displaystyle\frac{2}{3}\vec{q})\)

\(\vec{p}-(\displaystyle\frac{4}{3}k-1)\vec{a}=(\displaystyle\frac{2}{3}k+1)\vec{q}\)

両辺大きさをとって
\(|\vec{p}-(\displaystyle\frac{4}{3}k-1)\vec{a}|=|(\displaystyle\frac{2}{3}k+1)\vec{q}|\)

\(|\vec{q}|=1\) だから
\(|\vec{p}-(\displaystyle\frac{4}{3}k-1)\vec{a}|=|\displaystyle\frac{2}{3}k+1|\)
\(k>0\)より
\(|\vec{p}-(\displaystyle\frac{4}{3}k-1)\vec{a}|=\displaystyle\frac{2}{3}k+1\)

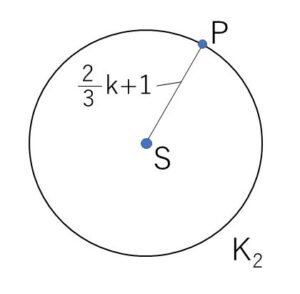
ここで、\((\displaystyle\frac{4}{3}k-1)\vec{a}=\overrightarrow{OS}\) とおくと

\(|\overrightarrow{OP}-\overrightarrow{OS}|=\displaystyle\frac{2}{3}k+1\)
\(|\overrightarrow{SP}|=\displaystyle\frac{2}{3}k+1\)・・・①

\(\displaystyle\frac{2}{3}k+1=(一定)>0\) だから、①は点\(P\)が点\(S\)を中心とする円周上を動くことを表している。

したがって
中心の位置ベクトル: \(\overrightarrow{OS}\)\(=(\displaystyle\frac{4}{3}k-1)\vec{a}\)
半径: \(\displaystyle\frac{2}{3}k+1\)

(3)

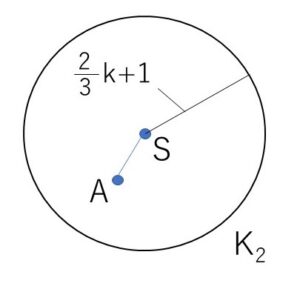
\(|\overrightarrow{AS}|\)
\(=|(\displaystyle\frac{4}{3}k-1)\vec{a}-\vec{a}|\)
\(=|(\displaystyle\frac{4}{3}k-2)\vec{a}|\)
\(=|\displaystyle\frac{4}{3}k-2|\)　(\(∵|\vec{a}|=1\))

円\(K_2\)の内部に点\(A\)が含まれるためには
\(|\overrightarrow{AS}|<\displaystyle\frac{2}{3}k+1\)
つまり
\(|\displaystyle\frac{4}{3}k-2|<\displaystyle\frac{2}{3}k+1\)

よって
\(-(\displaystyle\frac{2}{3}k+1)<\displaystyle\frac{4}{3}k-2<\displaystyle\frac{2}{3}k+1\) を解くと

\(\displaystyle\frac{1}{2}<k<\displaystyle\frac{9}{2}\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→法線ベクトルと直線の方程式　back→直線の方程式