法線ベクトルと直線の方程式の関係性について見ていきます。
・垂直な直線のベクトル方程式
定点\(A(\vec{a})\)を通り、\(\vec{0}\)でないベクトル\(\vec{n}\)に垂直な直線のベクトル方程式を考えます。
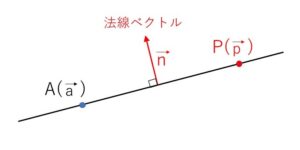
直線上の点を\(P(\vec{p})\)とすれば、図より
「\(\overrightarrow{AP} \perp \vec{n}\) または \(\overrightarrow{AP}=\vec{0}\) (\(P\)が\(A\)に一致)」
となるので
\(\vec{n}\cdot\overrightarrow{AP}=0\)
つまり求める直線のベクトル方程式は次のようになります。
\(\vec{n}\cdot(\vec{p}-\vec{a})=0\)・・・① (\(\vec{n}\)に垂直な直線のベクトル方程式)
このとき、垂直なベクトル\(\vec{n}\)を直線①の法線ベクトルとよびます。
ここで、\(P(x,y)\), \(A(x_0,y_0)\), \(\vec{n}=(a,b)\) とすると、
原点を基準として、\(\vec{p}=(x,y)\), \(\vec{a}=(x_0,y_0)\) と成分表示できるので①より
\((a,b)\cdot(x-x_0,y-y_0)=0\)
\(a(x-x_0)+b(y-y_0)=0\)
\(ax+by-ax_0-by_0=0\)
定数部分を \(c=-ax_0-by_0\) とおけば
\(ax+by+c=0\)・・・②
と見慣れた直線の方程式となります。すると②の形で表された直線の法線ベクトルが、\(\vec{n}=(a,b)\) と\(x,y\)の係数をそのままとったものであることが分かります。
・点と直線の距離(ベクトルによる証明)
点\(A(x_1,y_1)\) と、直線 \(ax+by+c=0\) の距離\(d\)は
\(d=\displaystyle\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
と表されますが、この公式はベクトルを利用しても導くことができます。
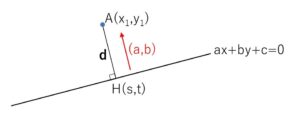
原点\((0,0)\)を\(O\)、\(A\)から直線に下した垂線の足を\(H(s,t)\)とします。
直線の法線ベクトルは \(\vec{n}=(a,b)\) であり
\(\overrightarrow{AH}/\!/\vec{n}\) より
\(\overrightarrow{AH}=k\vec{n}\)
\(\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{AH}\)
\(=(x_1,y_1)+k(a,b)\)
\(=(x_1+ka,y_1+kb)\)
\(\overrightarrow{OH}=(s,t)\) なので
\(s=x_1+ka\)・・・(i)
\(t=y_1+kb\)・・・(ii)
\(H(s,t)\)は直線上の点だから
\(as+bt+c=0\)・・・(iii)
(i),(ii)を(iii)に代入して
\(a(x_1+ka)+b(y_1+kb)+c=0\)
\(k\)について解くと
\(k=-\displaystyle\frac{ax_1+by_1+c}{a^2+b^2}\)
(\(ax+by+c=0\)が直線を表しているので、\((a,b)≠(0,0)\))
よって
\(|\overrightarrow{AH}|\)
\(=|k\vec{n}|\)
\(=|k||\vec{n}|\)
\(=\left|-\displaystyle\frac{ax_1+by_1+c}{a^2+b^2}\right|×\sqrt{a^2+b^2}\)
\(=\displaystyle\frac{|ax_1+by_1+c|}{a^2+b^2}×\sqrt{a^2+b^2}\)
\(=\displaystyle\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
(例題1)
(1)\(B(\vec{b})\), \(C(\vec{c})\) とする。線分\(BC\)の垂直二等分線のベクトル方程式を求めよ。
(2)2直線 \(x+2y+5=0\), \(x-3y+1=0\) のなす角\(θ\)を求めよ。
(解答)
(1)
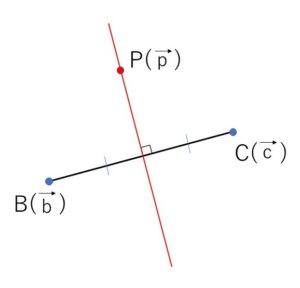
\(BC\)の中点の位置ベクトルは \(\displaystyle\frac{\vec{b}+\vec{c}}{2}\)
垂直二等分線は、\(BC\)の中点を通り\(BC\)に垂直なので直線上の点を\(P(\vec{p})\)とすれば
\((\vec{p}-\displaystyle\frac{\vec{b}+\vec{c}}{2})\cdot(\vec{c}-\vec{b})=0\)
(2)
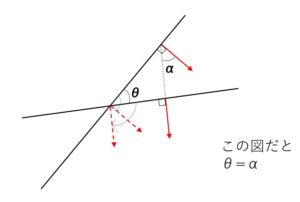
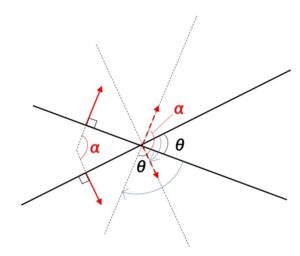
2直線を同じ方向に90°回転させることにより、それぞれの法線ベクトルに重ねることができるので、法線ベクトルのなす角を考えればよいことになります。
ただし、一般的に2直線のなす角\(θ\)は \(0°≦θ≦90°\) の範囲にとるので、ベクトルのなす角\(α\)が\(90°\)を超える場合には(\(\cosα\)が負になる場合)、\(180°\)からなす角\(α\)を引くことになります。
なお \(ax+by+c=0\) の法線ベクトル \((a,b)\) は1通りに方向が決まりますが、同じ大きさの垂直なベクトルはこの法線ベクトルと反対向きに存在します。仮に反対方向に法線ベクトルが位置していても、同様に2直線を同じ方向に90°回転させて重ねることができます。
\(x+2y+5=0\), \(x-3y+1=0\) の法線ベクトルは
\(\vec{n_1}=(1,2)\), \(\vec{n_2}=(1,-3)\)
法線ベクトルのなす角を\(α\)とすると
\(\cosα=\displaystyle\frac{1\cdot1+2\cdot(-3)}{\sqrt{1^2+2^2}\cdot\sqrt{1^2+(-3)^2}}\)
\(=-\displaystyle\frac{1}{\sqrt{2}}\)
よって \(α=135°\)
なす角\(θ\)は
\(θ=180-135°\)\(=45°\)
(例題2)
\(xy\)平面の点 \(O(0,0)\), \(A(1,1)\), \(B(2,-1)\) と実数\(k\)に対して、点\(C\)は
\(\overrightarrow{OC}=\overrightarrow{OB}+k\overrightarrow{OA}\)
を満たすとする。このとき、内積 \((\overrightarrow{OP}-\overrightarrow{OB})\cdot\overrightarrow{OA}\) が\(2k\)となる点\(P\)の描く図形は、\(C\)を通り、直線\(OA\)と直交する直線であることを示せ。
よって条件式から \(\overrightarrow{OB}\) を消去します。
(解答)
\((\overrightarrow{OP}-\overrightarrow{OB})\cdot\overrightarrow{OA}=2k\) より
\(\overrightarrow{OP}\cdot\overrightarrow{OA}-\overrightarrow{OB}\cdot\overrightarrow{OA}=2k\)
条件式 \(\overrightarrow{OB}=\overrightarrow{OC}-k\overrightarrow{OA}\) を代入して
\(\overrightarrow{OP}\cdot\overrightarrow{OA}-(\overrightarrow{OC}-k\overrightarrow{OA})\cdot\overrightarrow{OA}=2k\)
\(\overrightarrow{OP}\cdot\overrightarrow{OA}-\overrightarrow{OC}\cdot\overrightarrow{OA}+k|\overrightarrow{OA}|^2=2k\)
\(\overrightarrow{OA}=(1,1)\) より \(|\overrightarrow{OA}|^2=2\) だから
\((\overrightarrow{OP}-\overrightarrow{OC})\cdot\overrightarrow{OA}+2k=2k\)
\(\overrightarrow{CP}\cdot\overrightarrow{OA}=0\)
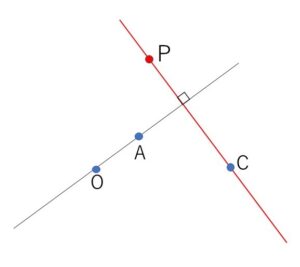
よって、\(\overrightarrow{CP} \perp \overrightarrow{OA}\) または \(\overrightarrow{CP}=\vec{0}\) となるので
\(P\)は\(C\)を通り、直線\(OA\)と直交する直線を描く。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→円の接線の方程式 back→円の方程式