円の接線の方程式

円の接線のベクトル方程式について見ていきます。

・円の接線のベクトル方程式
中心\(C(\vec{c})\)、半径\(r\)の円周上の点\(P_0(\vec{p_0})\)における円の接線の方程式を考えます。
接線上の点を\(P(\vec{p})\)として

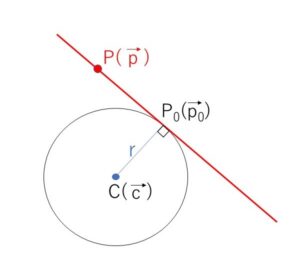
図より
\(\overrightarrow{CP_0} \perp \overrightarrow{P_0P}\)　または　\(\overrightarrow{P_0P}=\vec{0}\)
となるから

\(\overrightarrow{CP_0}\cdot\overrightarrow{P_0P}=0\)
\((\vec{p_0}-\vec{c})\cdot(\vec{p}-\vec{p_0})=0\)・・・①

\((\vec{p_0}-\vec{c})\cdot\{(\vec{p}-\vec{c})-(\vec{p_0}-\vec{c})\}=0\)
\((\vec{p_0}-\vec{c})\cdot(\vec{p}-\vec{c})-|\vec{p_0}-\vec{c}|^2=0\)

\(r=|\vec{p_0}-\vec{c}|\) より

\((\vec{p_0}-\vec{c})\cdot(\vec{p}-\vec{c})=r^2\)・・・②　(接線のベクトル方程式)

ここで座標平面上の原点を基準として、
\(\vec{p}=(x,y)\),　\(\vec{p_0}=(x_0,y_0)\)　\(\vec{c}=(a,b)\) とすると②より

\((x_0-a,y_0-b)\cdot(x-a,y-b)=r^2\)
\((x_0-a)(x-a)+(y_0-b)(y-b)=r^2\)

となり、特に \((a,b)=(0,0)\) (原点中心の円) とすると
\(x_0x+y_0y=r^2\)

と見慣れた式になります。

(例題)
平面上に点\(O\)を中心とする半径\(1\)の円\(C\)がある。円周上に直径の両端でない相異なる2点\(A,B\)をとり、\(\overrightarrow{OA}=\vec{a}\), \(\overrightarrow{OB}=\vec{b}\) とする。

(1)\(A,B\)における円\(C\)の接線の交点を\(P\)とし、\(\overrightarrow{OP}=\vec{p}\) とおくとき、
\(\vec{p}=\displaystyle\frac{1}{1+\vec{a}\cdot\vec{b}}(\vec{a}+\vec{b})\)を示せ。ただし、\(\vec{a}\cdot\vec{b}\) は \(\vec{a}\)と\(\vec{b}\)の内積を表す。

(2)この平面上の点\(Q\)に対して、\(\overrightarrow{OQ}=\vec{q}\) とする。\(\vec{q}=s\vec{a}+t\vec{b}\) とおいて \(\vec{p}\cdot\vec{q}\) を計算し、\(Q\)が直線\(AB\)上にあるための必要十分条件が \(\vec{p}\cdot\vec{q}=1\) であることを示せ。

(3)点\(Q\)が円\(C\)の外部で直線\(AB\)上にあるとき、\(Q\)から円\(C\)に引いた2つの接線の接点を\(D,E\)とすると、\(P,D,E\)は一直線上にあることを示せ。

(解答)
(1)

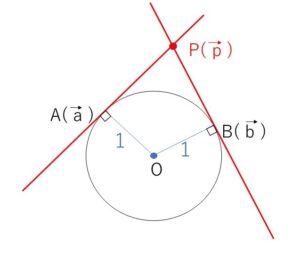
\(\vec{p}=m\vec{a}+n\vec{b}\) とおく。

\(A,B\)は接点だから
\((\vec{p}-\vec{a})\cdot\vec{a}=0\)
\((\vec{p}-\vec{b})\cdot\vec{b}=0\)

\((m|\vec{a}|^2+n\vec{a}\cdot\vec{b})-|\vec{a}|^2=0\)
\((m\vec{a}\cdot\vec{b}+n|\vec{b}|^2)-|\vec{b}|^2=0\)

\(m+n\vec{a}\cdot\vec{b}=1\)・・・①
\(m\vec{a}\cdot\vec{b}+n=1\)・・・②

①×\((\vec{a}\cdot\vec{b})\)－②より
\(n(\vec{a}\cdot\vec{b})^2-n=\vec{a}\cdot\vec{b}-1\)
\(n(\vec{a}\cdot\vec{b}+1)(\vec{a}\cdot\vec{b}-1)=\vec{a}\cdot\vec{b}-1\)・・・③

ここで\(A,B\)が異なる点で、\(AB\)は円の直径ではないことから、\(\vec{a},\vec{b}\)のなす角は\(0°\), \(180°\) とならないので
\(\vec{a}\cdot\vec{b}≠±|\vec{a}||\vec{b}|\)
つまり
\(\vec{a}\cdot\vec{b}≠±1\)

よって③より
\(n=\displaystyle\frac{1}{\vec{a}\cdot\vec{b}+1}\)

これと①より
\(m\)\(=1-\displaystyle\frac{\vec{a}\cdot\vec{b}}{\vec{a}\cdot\vec{b}+1}\)\(=\displaystyle\frac{1}{\vec{a}\cdot\vec{b}+1}\)

したがって
\(\vec{p}=\displaystyle\frac{1}{\vec{a}\cdot\vec{b}+1}(\vec{a}+\vec{b})\)

(2)

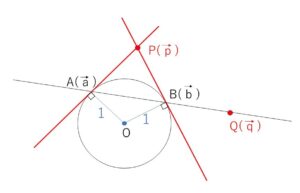
\(\vec{p}\cdot\vec{q}\)
\(=\displaystyle\frac{1}{\vec{a}\cdot\vec{b}+1}×(\vec{a}+\vec{b})\cdot(s\vec{a}+t\vec{b})\)

\(=\displaystyle\frac{1}{\vec{a}\cdot\vec{b}+1}×\{s|\vec{a}|^2+(s+t)\vec{a}\cdot\vec{b}+t|\vec{b}|^2\}\)

\(=\displaystyle\frac{1}{\vec{a}\cdot\vec{b}+1}×\{(s+t)(1+\vec{a}\cdot\vec{b})\}\)

\(=s+t\)

\(Q\)が直線\(AB\)上にあるための必要十分条件は \(s+t=1\) だから
\(\vec{p}\cdot\vec{q}=1\) が必要十分条件になる。

(3)

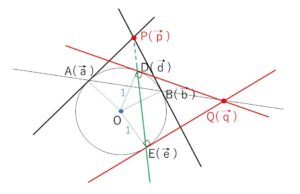
\(Q\)は\(AB\)上にあるので、(2)より \(\vec{p}\cdot\vec{q}=1\)・・・(※)

また、\(D(\vec{d}),E(\vec{e})\) とおくとこれらは\(Q\)を通る接線の接点だから、\(DE\)は直径にならない。よって 「\(\vec{a}→\vec{d}\), \(\vec{b}→\vec{e}\), \(\vec{p}→\vec{q}\), \(\vec{q}→\vec{p}\) 」とおきかえて(1)(2)と同様の議論をすると、\(P\)が\(DE\)上にある必要十分条件は

\(\vec{q}\cdot\vec{p}=1\)

これは(※)より成り立つので、\(P,D,E\)は一直線上にある。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→軌跡・領域①(線分・三角形,平行四辺形の内部)　back→法線ベクトルと直線の方程式