線分・三角形,平行四辺形の内部を表すベクトル方程式の演習です。
(例題1)
定三角形\(ABC\)がある。実数\(k\)に対して、点\(P\)が
\(\overrightarrow{PA}+2\overrightarrow{PB}+3\overrightarrow{PC}=k\overrightarrow{AB}\)
を満たしている。
(1)\(k\)が実数全体を動くとき、点\(P\)の軌跡を求めよ。
(2)点\(P\)が三角形\(ABC\)の内部にあるような\(k\)の値の範囲を求めよ。
(解答)
(1)
\(\overrightarrow{PA}+2\overrightarrow{PB}+3\overrightarrow{PC}=k\overrightarrow{AB}\) より
\(-\overrightarrow{AP}+2(\overrightarrow{AB}-\overrightarrow{AP})+3(\overrightarrow{AC}-\overrightarrow{AP})=k\overrightarrow{AB}\)
よって
\(\overrightarrow{AP}=\displaystyle\frac{1}{2}\overrightarrow{AC}+\displaystyle\frac{2-k}{6}\overrightarrow{AB}\)
したがって\(P\)の軌跡は
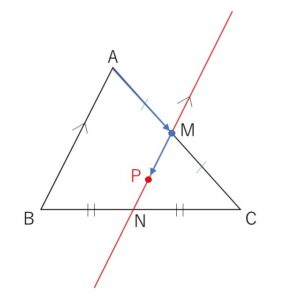
辺\(AC\)の中点を通り、辺\(AB\)に平行な直線。
(2)
または図形から判断して説くこともできます(別解)。
(1)より、\(P\)が三角形\(ABC\)の内部にある条件は
\(\displaystyle\frac{1}{2}>0\), \(\displaystyle\frac{2-k}{6}>0\), \(0<\displaystyle\frac{1}{2}+\displaystyle\frac{2-k}{6}<1\)
2番目の式から \(k<2\)
3番目の式から \(-1<k<5\)
したがって
\(-1<k<2\)
(別解)

\(P\)の軌跡である直線は、\(AC\)の中点\(M\)を通り、\(AB\)に平行だから
軌跡の直線と\(BC\)の交点は\(BC\)の中点\(N\)となる。
よって \(MN=\displaystyle\frac{1}{2}AB\) となるから、\(P\)が三角形の内部にあるつまり線分\(MN\)上(\(M,N\)を除く)にある条件は
\(\overrightarrow{AP}=\displaystyle\frac{1}{2}\overrightarrow{AC}+\displaystyle\frac{2-k}{6}\overrightarrow{AB}\) より
\(0<\displaystyle\frac{2-k}{6}<\displaystyle\frac{1}{2}\)
したがって
\(-1<k<2\)
(例題2)
三角形\(OAB\)がある。\(\overrightarrow{OP}=α\overrightarrow{OA}+β\overrightarrow{OB}\) で表されるベクトル\(\overrightarrow{OP}\)の終点\(P\)の集合は、\(α,β\)が次の条件をみたすとき、それぞれどのような図形を表すか。\(O,A,B\)を適当にとって図示せよ。
(1)\(\displaystyle\frac{α}{2}+\displaystyle\frac{β}{3}=1\), \(α≧0\), \(β≧0\) のとき
(2)\(1≦α+β≦2\), \(0≦α≦1\), \(0≦β≦1\) のとき
(3)\(β-α=1\), \(α≧0\) のとき
(解答)
(1)
\(\overrightarrow{OP}=α\overrightarrow{OA}+β\overrightarrow{OB}\)
\(=\displaystyle\frac{α}{2}(2\overrightarrow{OA})+\displaystyle\frac{β}{3}(3\overrightarrow{OB})\)
\(\displaystyle\frac{α}{2}+\displaystyle\frac{β}{3}=1\), \(\displaystyle\frac{α}{2}≧0\), \(\displaystyle\frac{β}{3}≧0\) より
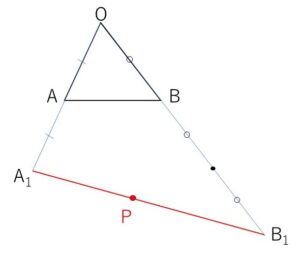
\(2\overrightarrow{OA}=\overrightarrow{OA_1}\), \(3\overrightarrow{OB}=\overrightarrow{OB_1}\) とおくと
\(P\)は線分\(A_1B_1\)上を動く。
よって図示すると次の通り。
(2)
また、別解としては条件を分けて考える方法がありますがこちらのほうが楽です。
条件「\(1≦α+β≦2\), \(0≦α≦1\), \(0≦β≦1\)」において
\(α+β=k\) (\(1≦k≦2\)) とおく。
\(α=k-β\) より、\(0≦k-β≦1\)
つまり \(k-1≦β≦k\)
\(1≦k≦2\) に注意して \(0≦β≦1\) と合わせると
\(k-1≦β≦1\)
\(\overrightarrow{OP}=α\overrightarrow{OA}+β\overrightarrow{OB}\)
\(=(k-β)\overrightarrow{OA}+β\overrightarrow{OB}\)
\(=k\overrightarrow{OA}+β\overrightarrow{AB}\)
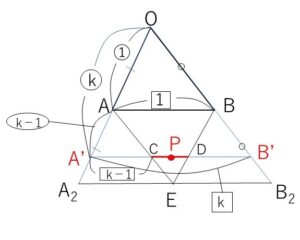
ここで、\(\overrightarrow{OA_2}=2\overrightarrow{OA}\), \(\overrightarrow{OB_2}=2\overrightarrow{OB}\) を満たすように\(A_2,B_2\)をとり、
\(A\)を通り\(OB\)に平行な直線と、\(B\)を通り\(OA\)に平行な直線をひきその交点を\(E\)とすると、\(E\)は\(A_2B_2\)の中点になる。
また、\(\overrightarrow{OA’}=k\overrightarrow{OA}\), \(\overrightarrow{OB’}=k\overrightarrow{OB}\) を満たすように\(A’,B’\)をとり、線分\(A’B’\)と\(AE,BE\)の交点をそれぞれ\(C,D\)とすれば
\(OA:OA’:AA’=1:k:k-1\), \(AB:A’B’:A’C=1:k:k-1\)
したがって
\(\overrightarrow{OP}=k\overrightarrow{OA}+β\overrightarrow{AB}\) (\(k-1≦β≦1\))
を満たす\(P\)は、線分\(CD\)上を動く。
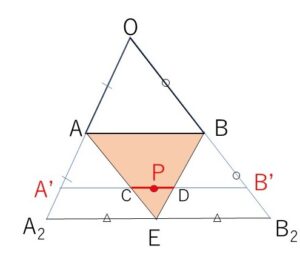
そして\(1≦k≦2\)の範囲で、\(A’\)は \(A\)から\(A_2\)の間を動くので\(P\)の描く図形は
三角形\(ABE\)の周および内部になる。図示すると次の通り。
(別解)
「\(1≦α+β≦2\) (\(α,β\)個別では制限なし)」と「\(0≦α≦1\), \(0≦β≦1\)」
に分けます。
まず 「\(1≦α+β≦2\)」 の表す領域を考える。
\(α+β=k\) (\(1≦k≦2\)) とおくと
\(\displaystyle\frac{α}{k}+\displaystyle\frac{β}{k}=1\)
\(\overrightarrow{OP}=α\overrightarrow{OA}+β\overrightarrow{OB}\)
\(=\displaystyle\frac{α}{k}(k\overrightarrow{OA})+\displaystyle\frac{β}{k}(k\overrightarrow{OB})\)
\(k\overrightarrow{OA}=\overrightarrow{OA’}\), \(k\overrightarrow{OB}=\overrightarrow{OB’}\) とおくと
\(P\)は直線\(A’B’\)を動き、\(2\overrightarrow{OA}=\overrightarrow{OA_2}\), \(2\overrightarrow{OB}=\overrightarrow{OB_2}\) を満たすように\(A_2,B_2\)を定めると、\(1≦k≦2\) の範囲で直線\(A’B’\)を動かすと、直線\(AB\)と直線\(A_2B_2\)の間の領域(この2直線も含む)が\(P\)の動く範囲になり、図示すると次の通り。
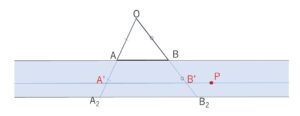
次に「\(0≦α≦1\), \(0≦β≦1\)」の表す領域を考えると
\(\overrightarrow{OE}=\overrightarrow{OA}+\overrightarrow{OB}\)
を満たすように\(E\)をとると(\(E\)は\(A_2B_2\)の中点)、\(P\)は平行四辺形\(OAEB\)の周および内部を動くので、領域を図示すると次の通り。
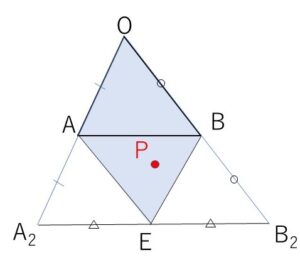
これら2つの領域の共通部分が求める図形になり、図示すると次の通り。
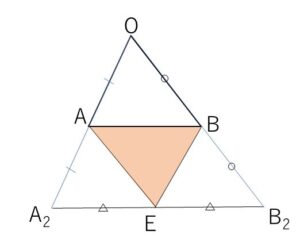
(注)\(α+β≦1\) の場合と比べると・・・
「\(0≦α+β≦1\), \(α≧0\), \(β≧0\) 」
は三角形\(OAB\)の周および内部を表しますが、
\(α+β≦1\) より \(α≦1\), \(β≦1\) となるので
「\(0≦α+β≦1\), \(0≦α≦1\), \(0≦β≦1\)」・・・①
も同じく三角形\(OAB\)の周および内部を表します。(つまり1以下の条件はあってもなくても同じ)
また、線分\(AB\)についても
「\(α+β=1\), \(α≧0\), \(β≧0\)」
「\(α+β=1\), \(0≦α≦1\), \(0≦β≦1\)」
のどちらも線分\(AB\)を表します。
ここで①において改めて \(α+β=k\)・・・② (\(0<k≦1\)) とおくと
\(\displaystyle\frac{α}{k}+\displaystyle\frac{β}{k}=1\)
また
\(\overrightarrow{OP}=\displaystyle\frac{α}{k}(k\overrightarrow{OA})+\displaystyle\frac{β}{k}(k\overrightarrow{OB})\)
の係数について、\(k≦1\)なので ②より\(α,β\)のとりうる値の最大値は\(k\)で
\(0≦α≦k\), \(0≦β≦k\) だから
\(0≦\displaystyle\frac{α}{k}≦1\), \(0≦\displaystyle\frac{β}{k}≦1\)
と\(0\)以上\(1\)以下の範囲にあるので線分全体を動くことになり問題ないのですが、
本問
「\(1≦α+β≦2\), \(0≦α≦1\), \(0≦β≦1\)」では
\(\overrightarrow{OP}=\displaystyle\frac{α}{k}(k\overrightarrow{OA})+\displaystyle\frac{β}{k}(k\overrightarrow{OB})\)
の係数について、\(k≧1\)なので 先ほどとは違い②において\(α,β\)のとりうる値の最大値は\(1\)で
\(0≦α≦1\), \(0≦β≦1\) となるので
\(0≦\displaystyle\frac{α}{k}≦\displaystyle\frac{1}{k}\), \(0≦\displaystyle\frac{β}{k}≦\displaystyle\frac{1}{k}\)
と\(k=1\)以外では、\(0\)以上\(1\)以下の範囲の一部となるので、線分の一部を動くことになります。
なお本問がもし「\(1≦α+β≦2\), \(α≧0\), \(β≧0\) 」と設定されていた場合には
\(α+β=k\) とおいたとき、\(0≦α≦k\), \(0≦β≦k\) となるから
線分全体を動くことになり、描く図形は台形になります。
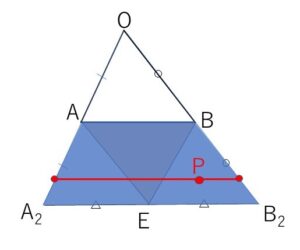
(3)
\(β-α=1\) より、\(β=α+1\)
\(\overrightarrow{OP}=α\overrightarrow{OA}+β\overrightarrow{OB}\)
\(=α\overrightarrow{OA}+(α+1)\overrightarrow{OB}\)
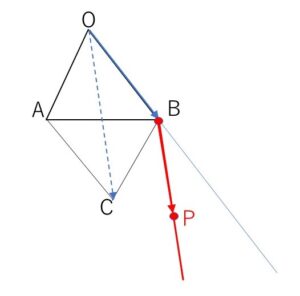
\(=\overrightarrow{OB}+α(\overrightarrow{OA}+\overrightarrow{OB})\) (文字\(α\)と定数で分けた)
ここで \(\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{OB}\)
とすれば、四角形\(OACB\)は平行四辺形で、\(OC\)は対角線になる。
したがって
\(\overrightarrow{OP}=\overrightarrow{OB}+α\overrightarrow{OC}\) と \(α≧0\) より
\(P\)の描く図形は\(B\)を端点とする\(OC\)に平行な半直線で、\(\angle AOB\) の内側にあるものになる。
これを図示すると次の通り。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→領域・軌跡③(座標の利用) back→軌跡・領域①(線分・三角形,平行四辺形の内部)