引き続き、ベクトルに関連する軌跡・領域の例題です。
(例題1)
平面上に \(BC=a\), \(CA=b\), \(AB=c\) である三角形\(ABC\)がある。その重心を\(G\)とし、\(\overrightarrow{GA}=\vec{α}\), \(\overrightarrow{GB}=\vec{β}\), \(\overrightarrow{GC}=\vec{γ}\) とする。
(1)\(\vec{α}\cdot\vec{α}+\vec{β}\cdot\vec{β}+\vec{γ}\cdot\vec{γ}\) および \(\vec{α}\cdot\vec{β}+\vec{β}\cdot\vec{γ}+\vec{γ}\cdot\vec{α}\) を\(a,b,c\)を用いて表せ。
(2)平面上の点\(P\)が \(\overrightarrow{PA}\cdot\overrightarrow{PB}+\overrightarrow{PB}\cdot\overrightarrow{PC}+\overrightarrow{PC}\cdot\overrightarrow{PA}=k\) (\(k\)は定数) をみたしながら動くとき、点\(P\)の軌跡を求めよ。
また辺の長さから
\(|\vec{β}-\vec{γ}|=a\), \(|\vec{γ}-\vec{α}|=b\), \(|\vec{α}-\vec{β}|=c\)・・・②③④
与式に合うように①~④を2乗して、それぞれの値を求めていきます。
(解答)
(1)
\(G\)は重心だから、\(\displaystyle\frac{\vec{α}+\vec{β}+\vec{γ}}{3}=\vec{0}\)、
つまり \(\vec{α}+\vec{β}+\vec{γ}=\vec{0}\)
よって
\((\vec{α}+\vec{β}+\vec{γ})\cdot(\vec{α}+\vec{β}+\vec{γ})=0\)
展開すると
\(\vec{α}\cdot\vec{α}+\vec{β}\cdot\vec{β}+\vec{γ}\cdot\vec{γ}+2(\vec{α}\cdot\vec{β}+\vec{β}\cdot\vec{γ}+\vec{γ}\cdot\vec{α})=0\)・・・①’
また
\(|\vec{β}-\vec{γ}|^2=a^2\)
\(|\vec{γ}-\vec{α}|^2=b^2\)
\(|\vec{α}-\vec{β}|^2=c^2\)
\(\vec{β}\cdot\vec{β}-2\vec{β}\cdot\vec{γ}+\vec{γ}\cdot\vec{γ}=a^2\)・・・②’
\(\vec{γ}\cdot\vec{γ}-2\vec{γ}\cdot\vec{α}+\vec{α}\cdot\vec{α}=b^2\)・・・③’
\(\vec{α}\cdot\vec{α}-2\vec{α}\cdot\vec{β}+\vec{β}\cdot\vec{β}=c^2\)・・・④’
②’+③’+④’ より
\(2(\vec{α}\cdot\vec{α}+\vec{β}\cdot\vec{β}+\vec{γ}\cdot\vec{γ})-2(\vec{α}\cdot\vec{β}+\vec{β}\cdot\vec{γ}+\vec{γ}\cdot\vec{α})=a^2+b^2+c^2\)・・・⑤
①’+⑤より
\(\vec{α}\cdot\vec{α}+\vec{β}\cdot\vec{β}+\vec{γ}\cdot\vec{γ}=\displaystyle\frac{a^2+b^2+c^2}{3}\)
①’より
\(\vec{α}\cdot\vec{β}+\vec{β}\cdot\vec{γ}+\vec{γ}\cdot\vec{α}=-\displaystyle\frac{a^2+b^2+c^2}{6}\)
(2)
\(\overrightarrow{GP}=\vec{p}\) とする。
\(\overrightarrow{PA}\cdot\overrightarrow{PB}+\overrightarrow{PB}\cdot\overrightarrow{PC}+\overrightarrow{PC}\cdot\overrightarrow{PA}=k\) より
\((\vec{α}-\vec{p})\cdot(\vec{β}-\vec{p})+(\vec{β}-\vec{p})\cdot(\vec{γ}-\vec{p})+(\vec{γ}-\vec{p})\cdot(\vec{α}-\vec{p})=k\)
\(3|\vec{p}|^2-2(\vec{α}+\vec{β}+\vec{γ})\cdot\vec{p}+(\vec{α}\cdot\vec{β}+\vec{β}\cdot\vec{γ}+\vec{γ}\cdot\vec{α})=k\)
よって(1)より
\(|\vec{p}|^2=\displaystyle\frac{1}{3}\left(k+\displaystyle\frac{a^2+b^2+c^2}{6}\right)\)
点\(P\)の軌跡は
(ア)\(k>-\displaystyle\frac{a^2+b^2+c^2}{6}\) のとき
\(G\)を中心とする、半径 \(\sqrt{\displaystyle\frac{1}{3}\left(k+\displaystyle\frac{a^2+b^2+c^2}{6}\right)}\) の円
(イ)\(k=-\displaystyle\frac{a^2+b^2+c^2}{6}\) のとき
点\(G\)
(ウ)\(k<-\displaystyle\frac{a^2+b^2+c^2}{6}\) のとき
なし
(例題2)
平面上において、点\(O\)を始点とする2つの半直線を\(l_1,l_2\)とし、それらのなす角は鋭角\(θ\) (\(0<θ<\displaystyle\frac{π}{2}\)) とする。
点\(A\)は\(l_1\)上の点で\(OA=1\)、点\(B\)は\(l_2\)上の点で\(OB=b\)とする。次に、直線\(AB\)上に点\(O\)から下ろした垂線と直線\(AB\)との交点を\(P\)とする。
(1)ベクトル\(\overrightarrow{OA},\overrightarrow{OB}\)によりベクトル\(\overrightarrow{OP}\) を
\(\overrightarrow{OP}=t\overrightarrow{OA}+(1-t)\overrightarrow{OB}\)
とするとき、\(t\)を\(b\)と\(θ\)を用いて表せ。
(2)\(θ\)を固定し、\(b\)を\(b>0\)の範囲で動かすとき、点\(P\)が\(l_1,l_2\)ではさまれる部分(ただし\(l_1,l_2\)も含む)にあるための\(b\)の範囲を求めよ。
(3)\(b\)が(2)で求めた範囲で動くとき、点\(P\)の描く軌跡と\(l_1,l_2\)で囲まれる部分の面積を求めよ。
(解答)
(1)
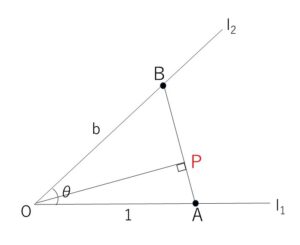
\(\overrightarrow{OP} \perp \overrightarrow{AB}\) より
\(\overrightarrow{OP}\cdot\overrightarrow{AB}=0\)
\(\{t\overrightarrow{OA}+(1-t)\overrightarrow{OB}\}\cdot(\overrightarrow{OB}-\overrightarrow{OA})=0\)
ここで、\(\overrightarrow{OA}\cdot\overrightarrow{OB}=b\cosθ\) だから
\(tb\cosθ-t+b^2(1-t)-(1-t)b\cosθ=0\)
(\(t\)について整理して)
\((b^2-2b\cosθ+1)t=b^2-b\cosθ\)
\(b^2-2b\cosθ+1=(b-\cosθ)^2-\cos^2θ+1\)
\(=(b-\cosθ)^2+\sin^2θ≠0\) (\(∵0<θ<\displaystyle\frac{π}{2}\)) より
\(t=\displaystyle\frac{b^2-b\cosθ}{b^2-2b\cosθ+1}\)
(2)
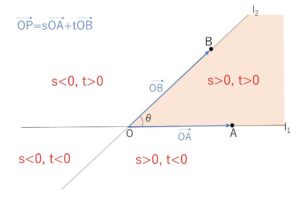
\(\overrightarrow{OP}=t\overrightarrow{OA}+(1-t)\overrightarrow{OB}\) に(1)の\(t\)を代入すると
\(\overrightarrow{OP}=\displaystyle\frac{b^2-b\cosθ}{b^2-2b\cosθ+1}\overrightarrow{OA}+\displaystyle\frac{-b\cosθ+1}{b^2-2b\cosθ+1}\overrightarrow{OB}\)
点\(P\)が\(l_1,l_2\)ではさまれる部分にあるためには
\(\displaystyle\frac{b^2-b\cosθ}{b^2-2b\cosθ+1}≧0\), \(\displaystyle\frac{-b\cosθ+1}{b^2-2b\cosθ+1}≧0\)
(1)より \(b^2-2b\cosθ+1>0\) だから
\(b(b-\cosθ)≧0\), \(-b\cosθ+1≧0\)
\(b>0\)より
\(\cosθ≦b≦\displaystyle\frac{1}{\cosθ}\)
(3)
\(\overrightarrow{OP}=\displaystyle\frac{b^2-b\cosθ}{b^2-2b\cosθ+1}\overrightarrow{OA}+\displaystyle\frac{-b\cosθ+1}{b^2-2b\cosθ+1}\overrightarrow{OB}\)
をそのまま利用して成分表示して座標で考える・・・などとすると大変です。そこでもともとの条件を思いだすと、\(\angle OPA=\displaystyle\frac{π}{2}\) (または\(P=A\))を満たしているので、\(P\)が\(OA\)を直径とする円を描くという平面幾何の基本的な定理を利用します。
ただこれだと(1)(2)の誘導があまり意味のない感じがしますが、(2)で\(b\)の範囲が分かっているのでより正確に軌跡を捉えることができるようになるぐらいに考えておきます。
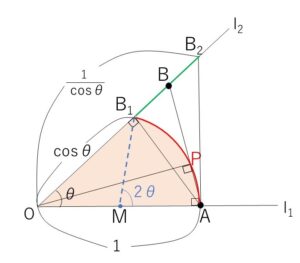
(2)で求めた範囲で\(b\)が動くとき
\(\angle OPA=\displaystyle\frac{π}{2}\) または \(P=A\) を満たすので
\(P\)は\(OA\)を直径とする円周の\(l_1,l_2\)ではさまれた部分を動く。
\(OA\)の中点を\(M\)、\(l_2\)上の\(O\)からの距離が\(\cosθ\)である点を\(B_1\)とすると、求める面積\(S\)は
\(S=△B_1OM+扇形AMB_1\)
\(=\displaystyle\frac{1}{2}(\cosθ)\cdot(\displaystyle\frac{1}{2})\cdot\sinθ+\displaystyle\frac{1}{2}\cdot(\displaystyle\frac{1}{2})^2\cdot2θ\)
\(=\displaystyle\frac{1}{8}\sin2θ+\displaystyle\frac{1}{4}θ\)
次回の最初でベクトルや図形問題の解法のまとめをしておきます。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→領域・軌跡⑤(ベクトルの選択) back→領域・軌跡③(座標の利用)