複数の不等式を満たす解を求めるときは、まずそれぞれの不等式を解けばよく、最後にそれぞれの不等式の解の共通範囲を求めます。共通範囲は慣れないうちは数直線で考えましょう。
実際に問題を解いてみます。
(問題1)次の連立不等式を解け。
(1)\(
\begin{eqnarray}
\left\{
\begin{array}{1}
2(1-x)>-6-x \\
2x-3≧-9
\end{array}
\right.
\end{eqnarray}\)
(2)\(
\begin{eqnarray}
\left\{
\begin{array}{1}
3x-2<x+4 \\
x-1<2x-6
\end{array}
\right.
\end{eqnarray}\)
(解答)
(1)\(2(1-x)>-6-x\) から
\(2-2x>-6-x\)
よって
\(-x>-8\)
したがって
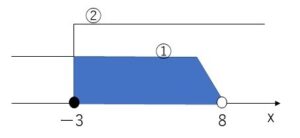
\(x<8\)・・・①
\(2x-3≧-9\)から
\(2x≧-6\)
したがって
\(x≧-3\)・・・②
①②から \(-3≦x<8\)
(2)\(3x-2<x+4\)より
\(2x<6\)
したがって
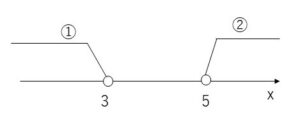
\(x<3\)・・・①
\(x-1<2x-6\)から
\(-x<-5\)
したがって
\(x>5\)・・・②
①②の共通部分はないので解なし。
(問題2)次の不等式を解け。
\(3x-7<x-1≦-x+3\)
\(A<B<C\)は、「\(A<B\) かつ \(B<C\)」と同値です。よって連立不等式、\(A<B,B<C\)と同じように解きます。ただし、「\(A<B,A<C\)」 や 「\(A<C,B<C\)」 と変形しないように。前者は\(B\)と\(C\)の大小、後者は\(A\)と\(B\)の大小が確定しないため、\(A<B<C\)と同値ではありません。
(解答)
\(3x-7<x-1\)から
\(2x<6\)
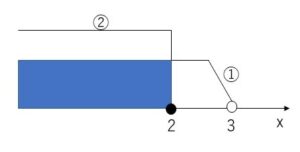
\(x<3\)・・・①
\(x-1≦-x+3\)から
\(2x≦4\)
\(x≦2\)・・・②
①②から \(x≦2\)
\(3x-7<x-1\)から
\(2x<6\)
\(x<3\)・・・①
\(x-1≦-x+3\)から
\(2x≦4\)
\(x≦2\)・・・②
①②から \(x≦2\)
以上になります。お疲れさまでした。
ここまで読んで頂きありがとうございました。