\(x\)の1次不等式の解は範囲となることが多いので、不等式を満たす\(x\)は無数に存在することになりますが、\(x\)が整数や自然数という条件がある場合、解が限られてきます。
次の①~③の例題を見ていきましょう。途中まではただ不等式を解けばいいだけです。
・①整数解を求める
(問題1)
不等式 \(3x<5x-2<x+12\)を満たす整数\(x\)をすべて求めよ。
(解答)
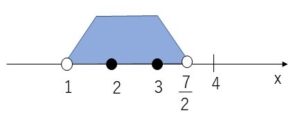
不等式を解くと(中略)、\(1<x<\displaystyle\frac{7}{2}\)
よって不等式を満たす整数は
\(x=2,3\)
・②最大(最小)の整数解と文字定数
(問題2)
\(4x<3a-2\)を満たす\(x\)の最大の整数値が\(5\)であるとき、定数\(a\)の値の範囲を求めよ。
(解答)
不等式を解くと \(x<\displaystyle\frac{3a-2}{4}\)
これを満たす最大の整数が\(5\)だから
\(5<\displaystyle\frac{3a-2}{4}≦6\)・・・(A)
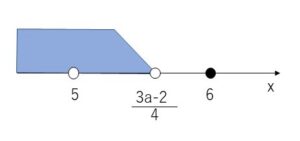
数直線から\(\displaystyle\frac{3a-2}{4}\)が5と6の間にありそうなのは分かりますが、境界は吟味しましょう。\(\displaystyle\frac{3a-2}{4}=5\)のときは、不等式が\(x<5\)となり最大の整数が4であるため(A)の左側の不等号の=はつきません。\(\displaystyle\frac{3a-2}{4}=6\)のときは、不等式が\(x<6\)となり最大の整数はちゃんと5になるので(A)の右側の不等号の=はつきます。
(A)を解くと(中略)
\(\displaystyle\frac{22}{3}<a≦\displaystyle\frac{26}{3}\)
\(\displaystyle\frac{22}{3}<a≦\displaystyle\frac{26}{3}\)
・③整数解の数と文字定数
(問題3)
次の連立不等式を満たす整数\(x\)がちょうど4個存在するような定数\(a\)の値の範囲を求めよ。
(問題3)
次の連立不等式を満たす整数\(x\)がちょうど4個存在するような定数\(a\)の値の範囲を求めよ。
\(
\begin{eqnarray}
\left\{
\begin{array}{1}
2x-3<x \\
2x-a>0
\end{array}
\right.
\end{eqnarray}\)
\begin{eqnarray}
\left\{
\begin{array}{1}
2x-3<x \\
2x-a>0
\end{array}
\right.
\end{eqnarray}\)
(解答)
\(2x-3<x\)から
\(x<3\)・・・(1)
\(2x-a>0\)から
\(x>\displaystyle\frac{a}{2}\)・・・(2)
\(2x-3<x\)から
\(x<3\)・・・(1)
\(2x-a>0\)から
\(x>\displaystyle\frac{a}{2}\)・・・(2)
(1)(2)よりちょうど4つの整数解をもつとき
解は \(x=-1,0,1,2\)となるので
\(-2≦\displaystyle\frac{a}{2}<-1\)・・・(B)
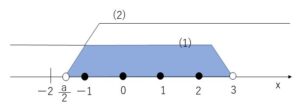
先ほどの(問題2)と同様に数直線で考えると、\(\displaystyle\frac{a}{2}\)が\(-2\)と\(-1\)の間になりそうです。境界を吟味すると、\(\displaystyle\frac{a}{2}=-2\)のとき不等式の解は、\(-2<x<3\)となり整数解は\(x=-1,0,1,2\) の4つとなるので(B)の左側の=はつきます。\(\displaystyle\frac{a}{2}=-1\)のときは不等式の解が、\(-1<x<3\)となり、整数解は\(x=0,1,2\)の3つしかないので(B)の右側の=はつきません。
(B)を解くと、両辺2倍して
\(-4≦a<-2\)
\(-4≦a<-2\)
以上になります。お疲れさまでした。
ここまで読んで下さりありがとうございました。
ここまで読んで下さりありがとうございました。