\(y=\displaystyle\frac{ax+b}{cx+d}\)
の形で表される分数関数(1次分数関数)のグラフの性質について見ていきます。
また、分数関数は微分(数Ⅲ)を用いても概形は分かりますが、2次関数のグラフを描くのに微分を用いないように、分数関数もその性質をおさえておきイメージできるようにしておきます。
・反比例のグラフ
\(k≠0\) として
\(y=\displaystyle\frac{k}{x}\) (\(xy=k\))
のグラフをおさらいしておきます。
簡単のため、
\(y=\displaystyle\frac{1}{x}\)・・・①
のグラフを代表例としてとりあげます。
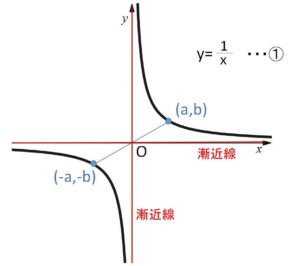
①のグラフと関数は、次のような特徴を持っています。
(1)第\(1\)象限と、第\(3\)象限に存在する。
(2)原点について対称である。
(3)漸近線は\(x\)軸(\(y=0\)) と \(y\)軸(\(x=0\))
(4)定義域は\(x=0\)を除くすべての実数、値域は\(0\)を除くすべての実数
(解説)
(1)
\(y=\displaystyle\frac{1}{x}\)・・・① について
\(x,y\)の符号が同じなので、グラフは第\(1\)象限と、第\(3\)象限に存在する。
(2)
点\((a,b)\)が①上にあるとき
\(b=\displaystyle\frac{1}{a}\)
が成り立つので、この式を両辺\(-1\)倍すると
\(-b=\displaystyle\frac{1}{-a}\)
よって、点\((-a,-b)\)も①上にあるから、原点対称のグラフとなる。
(3)
漸近線とは、曲線が限りなく近づくある一定の直線のことである。
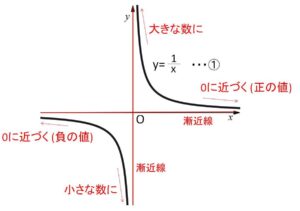
\(x\)を非常に大きくする、例えば \(x=1000000000\) とすると\(y\)の値は
\(y=\displaystyle\frac{1}{1000000000}\)
と\(0\)に近い正の値になる。よって\(x\)を大きくしていくと①のグラフは \(y=0\) (\(x\)軸)に近づく。同様に、\(x\)を非常に小さくする(\(x=-1000000000\)のような値を思い浮かべる)と\(y\)は\(0\)に近い負の値になるので、漸近線の1つは\(y=0\)となる。
また今度は、\(x=0\) に近い値について考える。
\(x=0.000000001\) のような\(0\)に近い正の値のとき、\(y\)は
\(y=\displaystyle\frac{1}{0.000000001}\)
と非常に大きな正の数になる。同様に\(x=-0.000000001\) のような\(0\)に近い負の値のとき、\(y\)は
\(y=-\displaystyle\frac{1}{0.000000001}\)
と非常に小さな負の数になる。よって漸近線は\(x=0\) (\(y\)軸) となる。
(正確には極限を考えることになる)
(4)
定義域は\(x=0\)だと分母が\(0\)になってしまうので、\(x=0\)を除くすべての実数。
また値域については、\(x\)にどのような実数を代入しても\(y\)は\(0\)にならないことと、その他の値 \(y=t\) については、\(t=\displaystyle\frac{1}{x}\) より \(x=\displaystyle\frac{1}{t}\) としてやれば \(y=t\) という値になるから、\(0\)を除くすべての実数になる。
(グラフから考えてもよい)
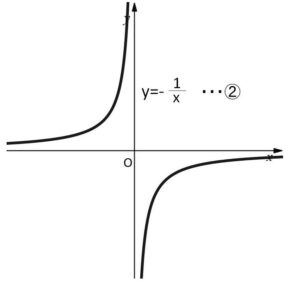
そして、\(y=-\displaystyle\frac{1}{x}\)・・・② については、第\(2\)象限、第\(4\)象限にグラフが存在すること以外は①と同様になり、一般的に \(y=\displaystyle\frac{k}{x}\) のグラフについては、\(k\)の正負によって①か②のどちらかの形状になります。
・\(y=\displaystyle\frac{k}{x-p}+q\) のグラフ
一般に、関数 \(y-q=f(x-p)\) (\(y=f(x-p)+q\))
のグラフは、\(y=f(x)\) のグラフを\(x\)軸方向に\(p\)、\(y\)軸方向に\(q\)だけ移動したものになるから
\(y=\displaystyle\frac{k}{x-p}+q\)・・・③
のグラフは、\(y=\displaystyle\frac{k}{x}\) のグラフを「\(x\)軸方向に\(p\)、\(y\)軸方向に\(q\)」だけ移動したものになります。よって、点\((p,q)\)をあたかも原点のように扱って反比例のグラフを考えればよいことになります。\(k>0\)のときの③のグラフと、その特徴をまとめると次の通りです。
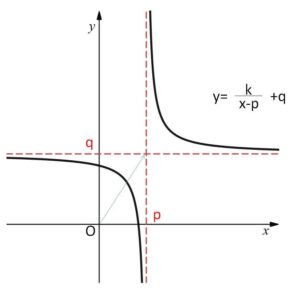
(i)点\((p,q)\)について対称である
(ii)漸近線は \(x=p\) と \(y=q\)
(iii)定義域は\(x=p\)を除くすべての実数、値域は\(q\)を除くすべての実数
・\(y=\displaystyle\frac{ax+b}{cx+d}\) について
\(ad-bc≠0\), \(c≠0\) として
\(y=\displaystyle\frac{ax+b}{cx+d}\)・・・④
のグラフは、式変形して \(y=\displaystyle\frac{k}{x-p}+q\) の形に帰着させます。
④は過分数の形になっているので、分子の次数を下げると (分子÷分母を計算してもよい)
\(y=\displaystyle\frac{\displaystyle\frac{a}{c}(cx+d)-\displaystyle\frac{ad}{c}+b}{cx+d}\)
\(=\displaystyle\frac{b-\displaystyle\frac{ad}{c}}{cx+d}+\displaystyle\frac{a}{c}\)
\(=\displaystyle\frac{bc-ad}{c^2(x+\displaystyle\frac{d}{c})}+\displaystyle\frac{a}{c}\)
\(=\displaystyle\frac{\displaystyle\frac{bc-ad}{c^2}}{x+\displaystyle\frac{d}{c}}+\displaystyle\frac{a}{c}\)
(\(y=\displaystyle\frac{k}{x-p}+q\) の形になっている)
(例題)
\(a\)を正の実数とする。\(x≧0\)のとき、\(y=\displaystyle\frac{ax-1}{a-x}\) がとりうる値の範囲を求めよ。
(解答)
\(y=\displaystyle\frac{ax-1}{a-x}\)
\(=\displaystyle\frac{-ax+1}{x-a}\)
\(=\displaystyle\frac{-a(x-a)-a^2+1}{x-a}\)
\(=\displaystyle\frac{1-a^2}{x-a}-a\) (\(x≧0\))
\(1-a^2≠0\) のときの漸近線は、\(x=a\), \(y=-a\) で、\(a>0\) より漸近線の交点(グラフの中心)は第\(4\)象限にあります。
(ア)\(a=1\) のとき
\(y=-1\) (定数関数)となるから、とりうる値は\(y=-1\)のみ
(イ)\(0<a<1\) のとき
\(y=\displaystyle\frac{1-a^2}{x-a}-a\)
において、\(1-a^2>0\) となり、定義域が\(x≧0\)だからグラフは次の通り
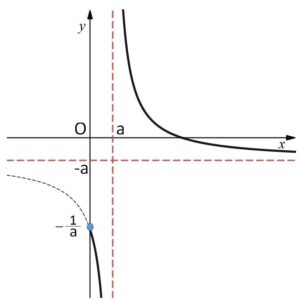
よってとりうる値の範囲は
\(y≦-\displaystyle\frac{1}{a}\), \(y>-a\)
(ウ)\(a>1\) のとき
\(1-a^2<0\) だからグラフは次の通り。
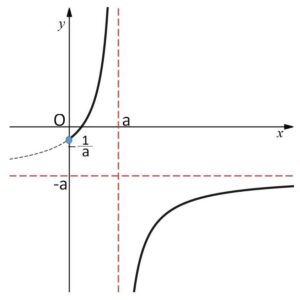
よってとりうる値の範囲は
\(y≧-\displaystyle\frac{1}{a}\), \(y<-a\)
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→分数方程式・不等式とグラフの共有点①