引き続き分数関数のグラフを利用する例題です。
(例題1)
\(a,b,c,d\)は実数で、\(ad-bc<0\), \(c≠0\) とする。このとき、次のことが成り立つことを証明せよ。
(1)\(x\)の方程式 \(\displaystyle\frac{ax+b}{cx+d}=x\) は相異なる2つの実数解をもつ。
(2) (1)の2解を\(α,β\) (\(α<β\)) とするとき、\(α<x<β\) かつ \(x≠-\displaystyle\frac{d}{c}\) ならば \(\displaystyle\frac{ax+b}{cx+d}<α\) または \(β<\displaystyle\frac{ax+b}{cx+d}\) である。
(解答)
(1)
\(\displaystyle\frac{ax+b}{cx+d}=x\) について
\(y=\displaystyle\frac{ax+b}{cx+d}\)
\(=\displaystyle\frac{\displaystyle\frac{a}{c}(cx+d)-\displaystyle\frac{ad}{c}+b}{cx+d}\)
\(=\displaystyle\frac{-(ad-bc)}{c^2(x+\displaystyle\frac{d}{c})}+\displaystyle\frac{a}{c}\)
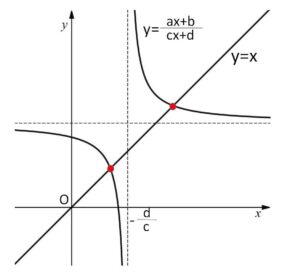
条件より \(\displaystyle\frac{-(ad-bc)}{c^2}>0\) だから、\(y=\displaystyle\frac{ax+b}{cx+d}\) のグラフは図のようになる。\(y=x\) のグラフもあわせて考えると2つの異なる交点をもつから、方程式は異なる2つの実数解をもつ。
(2)
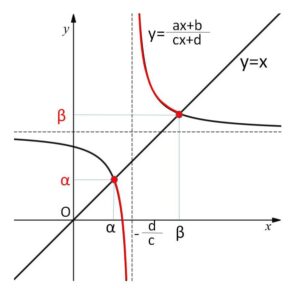
(1)の2つのグラフの交点は \((α,α)\) と \((β,β)\)。よってグラフから
\(α<x<β\) かつ \(x≠-\displaystyle\frac{d}{c}\) ならば \(\displaystyle\frac{ax+b}{cx+d}<α\) または \(β<\displaystyle\frac{ax+b}{cx+d}\)
(例題2)
(1)\(xy\)平面上に、曲線 \(xy=3x+2y-5\) のグラフをかけ。
(2)\(0<x≦a\), \(y>0\) である\(x,y\)が上の式を満たすとき、\(x+y\)が最大値をもつための\(a\)の条件を求めよ。また、そのときの最大値も求めよ。
(解答)
(1)
\(xy=3x+2y-5\) より
\((x-2)y=3x-5\)
ここで、\(x=2\) とすると、\(0=1\) となり等式が成り立たたないので、\(x≠2\)
よって
\(y=\displaystyle\frac{3x-5}{x-2}=\displaystyle\frac{3(x-2)+1}{x-2}\)
ゆえに
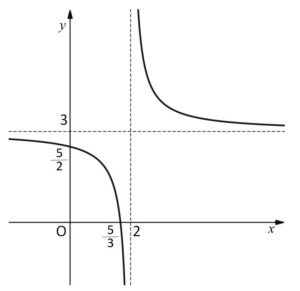
\(y=\displaystyle\frac{1}{x-2}+3\) のグラフをかくと次の通り。
(2)
漸近線が\(x=2\)になっているのでこれをまたぐように範囲をとるようにすると、例えば\(a=3\) のとき \(0<x≦3\) が範囲で、曲線の右上部分が\(x=2\)付近では限りなく大きくなるので、①と曲線が共有点を持つ場合の\(k\)の値も限りなく大きくなるので、最大値をもたないことになります。\(a=2\)だと範囲は\(0<x≦2\)となり左下の部分しか含まれないので、最大値をもつようになりこれが境目です。
\(0<x≦a\) より、\(a>0\)
\(x+y=k\)・・・①
とおいて、①と曲線が共有点をもつ場合を考える。
(i)\(a>2\)のとき
\(0<x≦a\), \(y>0\) において、\(x\)の値を\(2\)より大きい値から\(2\)に近づけると限りなく大きくなるので、直線①と曲線が交わるときの\(k\)の値も限りなく大きくできるため、最大値をもたず不適。
(ii)\(0<a≦2\)のとき
に着目しますが、①と曲線がこの範囲内で1点で交わる(接する)可能性もあるのでこれも調べます。このあたりの直線①と曲線の位置関係については厳密には凸性や曲線の接線の傾きに着目します(後程説明します)。
\(-x+k=\displaystyle\frac{3x-5}{x-2}\) について
両辺を\(x-2\)倍して
\((-x+k)(x-2)=3x-5\) (このとき\(x=2\)は解にならない)
整理すると
\(x^2+(1-k)x+2k-5=0\)
重解をもつときグラフの交点は1つになるから
\(D=(1-k)^2-4(2k-5)=0\)
\(k^2-10k+21=0\)
\((k-3)(k-7)=0\)
\(k=3,7\)
重解は\(x=\displaystyle\frac{k-1}{2}\)だから、\(0<x<2\)の範囲にあるのは
\(k=3\) のときで、1点で交わるときの交点の\(x\)座標は\(x=1\)
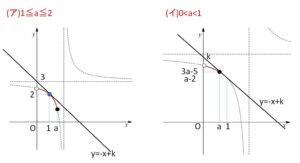
(ア)\(1≦a≦2\)のとき
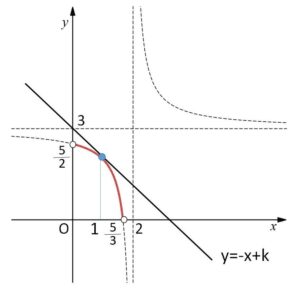
図より①の\(y\)切片\(k\)が最大となるのは、①が\((1,2)\)を通るときだから
最大値は \(k=1+2=\)\(3\)
(イ)\(0<a<1\)のとき
図より①の\(y\)切片\(k\)が最大となるのは、①が\((a,\displaystyle\frac{3a-5}{a-2})\)を通るときだから
最大値は \(k=a+\displaystyle\frac{3a-5}{a-2}=\)\(\displaystyle\frac{a^2+a-5}{a-2}\)
したがって最大値をもつ\(a\)の条件は
\(0<a≦2\) であり、そのときの最大値は上記の通り。
(注)
2階微分すると分かるが、\(x<2\) において曲線は上に凸のグラフ。よって直線①と曲線が1点で交わるとき、この交点以外では曲線は下側にある。よって(ア)において最大値をとるときは\(x=1\)のとき。
また、(イ)においては両端 \(x=0,a\) が候補。(\(x=0\)でもし最大値ならば範囲に含まれていないので最大値はなしになる)
\(x=1\)のときの曲線の接線の傾きは直線①と同じ\(-1\)で、上に凸のグラフで左にいくにつれて曲線の接線の傾きが緩やかになっていくので右端の\(x=a\)のとき最大値をとる。
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→分数関数と図形 back→分数方程式・不等式とグラフの共有点①