2次式の分数関数

今回は2次式を含む分数関数の例題です。

(例題1)
実数\(x\)は \(1<x<4\) かつ \(x≠2,3\) とする。このとき
\(y=\displaystyle\frac{2}{(x-1)(2-x)}+\displaystyle\frac{2}{(x-2)(3-x)}+\displaystyle\frac{2}{(x-3)(4-x)}\)
の\(y\)の最小値を求めよ。

(例題)
\(y=\displaystyle\frac{2}{(x-1)(2-x)}+\displaystyle\frac{2}{(x-2)(3-x)}+\displaystyle\frac{2}{(x-3)(4-x)}\)

\(=-\displaystyle\frac{2\{(x-3)(x-4)+(x-1)(x-4)+(x-1)(x-2)\}}{(x-1)(x-2)(x-3)(x-4)}\)

\(=-\displaystyle\frac{6(x^2-5x+6)}{(x-1)(x-2)(x-3)(x-4)}\)

\(=-\displaystyle\frac{6(x-2)(x-3)}{(x-1)(x-2)(x-3)(x-4)}\)

\(=-\displaystyle\frac{6}{(x-1)(x-4)}\)

\(=\displaystyle\frac{6}{-x^2+5x-4}\)

\(=\displaystyle\frac{6}{-(x-\displaystyle\frac{5}{2})^2+\displaystyle\frac{9}{4}}\)

\(1<x<4\) かつ \(x≠2,3\) のとき
\(0<-(x-\displaystyle\frac{5}{2})^2+\displaystyle\frac{9}{4}≦\displaystyle\frac{9}{4}\)

よって、\(y\)の値が最小となるのは \(x=\displaystyle\frac{5}{2}\) のときで
最小値は
\(y=\displaystyle\frac{6}{\displaystyle\frac{9}{4}}\)\(=\displaystyle\frac{8}{3}\)

(例題2)
\(f(x)=\displaystyle\frac{x^2+ax+b}{x^2-x+1}\)
の最大値が\(3\)、最小値が\(\displaystyle\frac{1}{3}\)である。このとき、\(a,b\)の値を求めよ。

(解答)
条件より、不等式
\(\displaystyle\frac{1}{3}≦\displaystyle\frac{x^2+ax+b}{x^2-x+1}≦3\)・・・①
が任意の実数\(x\)について成り立ち、かつ等号が成り立つ\(x\)が存在すればよい。

\(x^2-x+1=(x-\displaystyle\frac{1}{2})^2+\displaystyle\frac{3}{4}>0\)
だから①より中辺の分母を払って (不等号の向きが変わらず)
\(\displaystyle\frac{1}{3}(x^2-x+1)≦x^2+ax+b≦3(x^2-x+1)\)

整理すると
\(2x^2+(3a+1)x+3b-1≧0\)・・・②
かつ
\(2x^2-(a+3)+3-b≧0\)・・・③
となるから、②③が任意の実数\(x\)で成り立ち、等号が成立する\(x\)が存在すればよい。

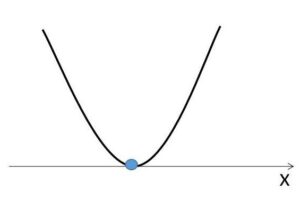
②③の \(y=(左辺)\) はどちらも2次関数で下に凸のグラフだから判別式から
\(D_1=(3a+1)^2-8(3b-1)=0\)
\(D_2=(a+3)^2-8(3-b)=0\)

よって
\((3a+1)^2+8=24b\)・・・④
\((a+3)^2-24=-8b\)・・・⑤

④+3×⑤ より
\((3a+1)^2+8+3(a+3)^2-72=0\)
\(12a^2+24a-36=0\)
\(a^2+2a-3=0\)
\((a+3)(a-1)=0\)
\(a=-3,1\)

⑤より
\(a=-3\) のとき \(b=3\)
\(a=1\) のとき \(b=1\)

以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→無理関数のグラフ　back→分数関数と図形