無理関数について見ていきます。
・無理関数(1次式の平方根)
\(y=\sqrt{2x}\) や \(y=\sqrt[3]{x^2+4}\) の右辺のような、根号の中に文字を含む式を無理式といい、また無理式で表された関数を無理関数といいます。ここでは、根号が平方根(2乗根)で文字式が1次式であるものを扱っていきますが、基本的な考え方は他の場合であっても同様です。
無理関数
\(y=\sqrt{x}\)・・・①
について、実数の範囲で考えると\(y\)が実数のとき\(x≧0\)だから、定義域は\(x≧0\)です。また値域は右辺の根号の符号は正または\(0\)なので、\(y≧0\)です。
このことを踏まえて①のグラフを考えるために①の両辺を\(2\)乗すると
\(y^2=x\) (\(y≧0\))
であり、この式を \(x=y^2\)・・・② と\(y\)の関数とみると2次関数になってます。
②のグラフは普段よく扱う\(x\)の2次関数の横方向を縦方向に変えれば描けるので、
\(y=\sqrt{x}\)・・・① のグラフは \(y≧0\) に注意すると次のようになります。
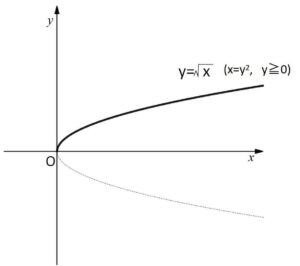
同様に、\(y=-\sqrt{x}\)・・・③ については、定義域が\(x≧0\) (①と同じ)、値域が\(y≦0\)。
③を2乗すると同じ \(y^2=x\)・・・② が得られるので③のグラフは次の通りです。
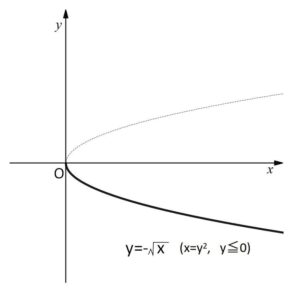
\(y=\sqrt{x}\) と \(y=-\sqrt{x}\) を合わせたものは \(y^2=x\)・・・② になるわけですが、これは
\(y^2=x\)
を\(y\)について解くと、\(y=±\sqrt{x}\) (\(x≧0\)) となることからも分かります。
・無理関数のグラフの移動
無理関数のグラフの対称移動・平行移動は一般の関数と同様です。
まず
\(y=\sqrt{-x}\)・・・④
についてですが、これは\(y=\sqrt{x}\)で \(x→-x\) としたものなので、「\(y=\sqrt{x}\)を\(y\)軸について対称移動」したグラフになります。このとき定義域は\(x≦0\)です。
\(y=-\sqrt{-x}\)・・・⑤
については、\(-y=\sqrt{-x}\)より「④のグラフを\(x\)軸について対称移動したもの」と考えてもよいですし、「\(y=-\sqrt{x}\)・・・③ を\(y\)軸について対称移動したもの」 or 「\(y=\sqrt{x}\)・・・①を原点について対称移動したもの」と考えてもよいです。
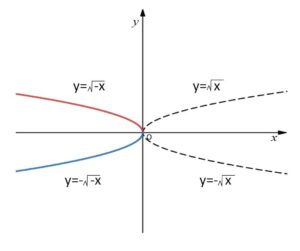
以上のことを踏まえると、\(y=±\sqrt{ax}\) (\(a≠0\)) のグラフは\(a\)の正負により上図の4つのパターンいずれかと同じ形状になることが分かります。
続いて平行移動についてですが、例えば
\(y=\sqrt{ax+b}+c\) (\(a≠0\))
のグラフは、\(y-c=\sqrt{a(x+\displaystyle\frac{b}{a})}\)
となることから、\(y=\sqrt{ax}\)のグラフを\(x\)軸方向に\(-\displaystyle\frac{b}{a}\)、\(y\)軸方向に\(c\)だけ平行移動したものになります。
(例題)
関数 \(y=f(x)=\sqrt{5x}\) がある。
(1)曲線\(y=f(x)\)と\(y\)軸に関して対称な曲線を\(y=g(x)\)とする。この曲線\(y=g(x)\)を\(x\)軸方向に\(10\)だけ平行移動した曲線を\(y=h(x)\)とする。\(y=h(x)\)を求めよ。
(2)関数\(y=f(x)\)と関数\(y=h(x)\)のグラフをかけ。
(解答)
(1)
\(y=f(x)\)を\(y\)軸について対称移動すると\(y=g(x)\)となるから
\(g(x)=\sqrt{5(-x)}=\sqrt{-5x}\)
よって
\(h(x)=\sqrt{-5(x-10)}\)
\(=\sqrt{-5x+50}\)
(2)
\(h(x)=\sqrt{-5(x-10)}\)
だから、定義域は\(x-10≦0\) より \(x≦10\)
\(y=\sqrt{5x}\) と \(y=\sqrt{-5(x-10)}\)のグラフは次の通り。
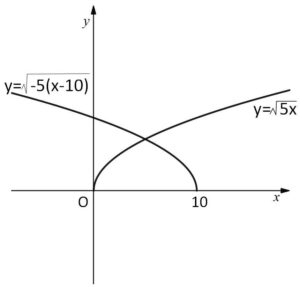
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→無理関数・方程式とグラフの共有点 back→2次式の分数関数