無理方程式と不等式に関する例題です。
(1)式変形して解く (2)グラフを考える
です。
(例題1)
次の不等式を解け。ただし\(x\)は実数とする。
\(\sqrt{2x+4}>\displaystyle\frac{2}{3}x\)
(解答1)式変形で解く
例えば両辺が\(0\)以上ならば2乗しても不等号は変わりませんが、負の値になるときには不等号が入れ替わる場合があります(\(3>-5\) のとき2乗すると \(9<25\))。なので2乗する前に符号を考慮します。
また、ルートの中身の正負にも注意です。
\(\sqrt{2x+4}>\displaystyle\frac{2}{3}x\)・・・① について
\(2x+4≧0\) より \(x≧-2\)
(i)\(-2≦x<0\) のとき
①の右辺は負の値だから、不等式は成り立つ。
したがって、\(-2≦x<0\) は解。
(ii)\(x≧0\) のとき
①の両辺を2乗して
\(2x+4>\displaystyle\frac{4}{9}x^2\)
\(2x^2-9x-18<0\)
\((2x+3)(x-6)<0\)
\(-\displaystyle\frac{3}{2}<x<6\)
よって、\(0≦x<6\) は解。
以上より不等式①の解は
\(-2≦x<6\)
(解答2)グラフを考える
\(\sqrt{2x+4}=\displaystyle\frac{2}{3}x\)・・・② を解く。
\(2x+4≧0\) より \(x≧-2\)
また②の左辺は\(0\)以上の値だから、\(x≧0\)
②の両辺を2乗して
\(2x+4=\displaystyle\frac{4}{9}x^2\)
整理して
\((2x+3)(x-6)=0\)
\(x≧0\) を満たすのは \(x=6\)
ちなみにもう1つの解 \(x=-\displaystyle\frac{3}{2}\) については、折り返したグラフ \(y=-\sqrt{2x+4}\) との交点の\(x\)座標です。
ここで
\(y=\sqrt{2x+4}=\sqrt{2(x+2)}\)
\(y=\displaystyle\frac{2}{3}x\)
のグラフを\(x≧-2\)の範囲でかくと次の通り。
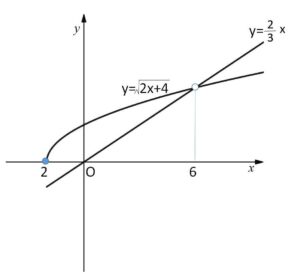
よって \(\sqrt{2x+4}>\displaystyle\frac{2}{3}x\) を満たす\(x\)は、無理関数が上側に位置する範囲を考えて
\(-2≦x<6\)
(例題2)
次の方程式の実数解の個数を調べよ。ただし\(k\)を実数の定数とする。
\(2\sqrt{x+4}=x+k\)
式変形だと平方根を解消するために2乗することになりますが、正負の条件を考慮する(\(x≧-k\)という文字式で表された範囲がでてくる)ことになるのでやや面倒です。
(解答)
\(y=2\sqrt{x+4}\)
\(y=x+k\)
のグラフをかくと次の通り。
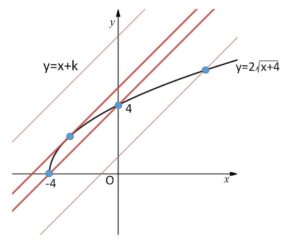
(まず共有点がなくなる境目を調べます)
\(2\sqrt{x+4}=x+k\)・・・①
①の両辺を2乗して
\(4(x+4)=(x+k)^2\)
\(x^2+2(k-2)x+k^2-16=0\)・・・②
判別式\(\displaystyle\frac{D}{4}=0\)より
\((k-2)^2-(k^2-16)=0\)
\(k=5\)
このとき①は \(2\sqrt{x+4}=x+5\)・・・③ となり、その解②より \(x=-(k-2)=-3\)
\(x=-3\) は③を満たすので、\(k=5\) のときは2つのグラフは1点のみで交わる。
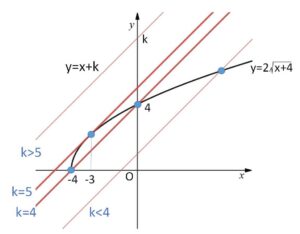
\(k=5,4\)が共有点の個数の変化の境目になっていて、
\(2\sqrt{x+4}=x+k\) の実数解の個数とグラフの共有点の個数は一致するから
\(k>5\) のとき なし
\(k=5\) のとき 1個
\(4≦k<5\) のとき 2個
\(k<4\) のとき 1個
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→円の方程式と無理関数 back→無理関数のグラフ