円の方程式と無理関数の関係について見ていきます。
・円の方程式と無理関数
\(x^2+y^2=r^2\)・・・① (\(r>0\))
は、座標平面上では原点を中心とする半径\(r\)の円を表します。①は\(x\)の関数でも\(y\)の関数でもありませんが、\(y\)について解くと
\(y^2=r^2-x^2\)
より、\(y^2≧0\) に注意すると、\(r^2-x^2≧0\) だから
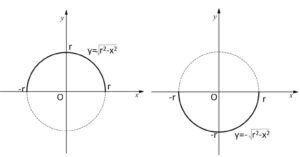
\(y=±\sqrt{r^2-x^2}\) (定義域は\(-r≦x≦r\))・・・②
と\(±\)の2式で分けることで\(y\)の関数で表すことができます。\(y\)の正負を考えると②の\(±\)のうち
\(y=\sqrt{r^2-x^2}\)
は円の上側半分を表し、
\(y=-\sqrt{r^2-x^2}\)
は円の下側半分を表すことが分かります。
(例題)
不等式 \(\sqrt{a^2-x^2}>3x-a\) (\(a≠0\)) の解は、\(a>0\)のとき ( ア )、\(a<0\)のとき ( イ ) である。
(解答)
\(y=\sqrt{a^2-x^2}\)・・・①
\(y=3x-a\)・・・②
について
(ア)\(a>0\)のとき
直線②の\(y\)切片は\(-a\)で負の値。直線②に\(x=a\)を代入すると\(y=2a\)となるから、半円①と合わせて図示すると次の通り。
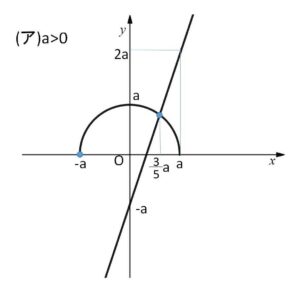
①②の交点の座標を求めると
\(\sqrt{a^2-x^2}=3x-a\)・・・③
2乗して
\(a^2-x^2=(3x-a)^2\)
整理すると
\(x(5x-3a)=0\)
\(x=0,\displaystyle\frac{3}{5}a\)
このうち③を満たすのは
\(x=\displaystyle\frac{3}{5}a\)
よって
\(\sqrt{a^2-x^2}>3x-a\)
を満たす\(x\)の範囲は、半円①が上側に位置する範囲より
\(-a≦x<\displaystyle\frac{3}{5}a\)
(イ)\(a<0\) のとき
直線②の\(y\)切片は\(-a\)で正の値で、この点 \((0,-a)\) は半円①も通る。
\(x=a\ (<0)\) を②に代入すると \(y=2a\ (<0)\) だから、①②を図示すると次の通り。
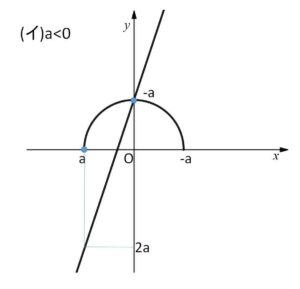
よって
\(\sqrt{a^2-x^2}>3x-a\)
を満たす\(x\)の範囲は
\(a≦x<0\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→逆関数の性質とグラフ back→無理方程式・不等式とグラフの共有点