\(2x+y=4\)・・・①
\(3x+2y=7\)・・・②
を同時に満たす\((x,y)\)を座標する点は①②の交点になりますが、これは連立方程式①②の解になります。実際方程式を解くと、\((x,y)=(1,2)\) となり、これが交点の座標です。
連立方程式を解く際には、倍数をとったり和・差を取ったりしますが、これと同じように和①+②、差①-② をとると
\(5x+3y=11\)・・・③
\(-x-y=-3\)・・・④
となります。このとき、①②から③④が得られるので「①かつ② \(→\) ③かつ④」は成り立ち、逆に ①+②=③、①-②=④ なので、(③+④)÷2=①、 (③-④)÷2=② であり③④から①②が求まるので「③かつ④ \(→\) ①かつ②」が成り立ちます。よって「①かつ② と ③かつ④」は同値となります。このように2式の和と差をとってできた2式は同値になるので(定数倍もしてもよい)、①②が仮に複雑な式の場合に簡単な式に同値性を保ったまま変形することができます。実際③④からも交点\((1,2)\) は求まります。
ちなみに、①②から連立方程式を解く操作が同値変形でどう表されるかというと
「①かつ② \(⇔\) ①かつ ①×2-②」
です。①×2-② より \(x=1\) が得られ、これを①に代入して \(y=2\) が得られるということです。
(例題)
\(k>0\) とする。\(xy\)平面上の二曲線
\(y=k(x-x^3)\), \(x=k(y-y^3)\)
が第\(1\)象限に \(α≠β\) なる交点 \((α,β)\) をもつような\(k\)の範囲を求めよ。
対称的な式なので、和や差をとって同値変形していきます。差をとると \(y-x\) という因数がでてきますが、これは2曲線が \(y=x\) について対称で、もし \(y=x\) と片方の曲線が交点をもてば2曲線が交点をもつことからも分かります。(この例題では \(y≠x\) ですが)
(解答)
\(y=k(x-x^3)\)・・・①
\(x=k(y-y^3)\)・・・②
①+②、①-②より
\(y+x=k(x+y)-k(x^3+y^3)\)
\(y-x=k(x-y)-k(x^3-y^3)\)
\(y+x=k(x+y)-k(x+y)(x^2-xy+y^2)\)
\(y-x=k(x-y)-k(x-y)(x^2+xy+y^2)\)
交点が第\(1\)象限にあるから \(x,y>0\) より、\(x+y≠0\)
また \(x≠y\) より、\(x-y≠0\)
よって
\(1=k-k(x^2-xy+y^2)\)・・・③
\(-1=k-k(x^2+xy+y^2)\)・・・④
さらに③+④、③-④より
\(0=2k-2k(x^2+y^2)\)
\(2=2kxy\)
\(k>0\)より
\(x^2+y^2=1\)・・・⑤
\(xy=\displaystyle\frac{1}{k}\)・・・⑥
「①かつ② \(⇔\) ③かつ④ \(⇔\) ⑤かつ⑥」
より、曲線⑤⑥が第\(1\)象限で\(y=x\)上にない交点をもてばよい。つまり⑤⑥を同時に満たす正の数\(x,y\) (\(x≠y\)) が存在する条件を求めればよい。
円と反比例のグラフの位置関係を考えてもよいです。
⑤より
\((x+y)^2-2xy=1\)
⑥を代入して
\((x+y)^2=1+\displaystyle\frac{2}{k}\)
\(x+y>0\)、\(k>0\) より
\(x+y=\sqrt{1+\displaystyle\frac{2}{k}}\)
よって\(t\)の方程式
\(t^2-\left(\sqrt{1+\displaystyle\frac{2}{k}}\right)t+\displaystyle\frac{1}{k}=0\)
が異なる正の実数解をもてばよく
(i)判別式 \(D=(1+\displaystyle\frac{2}{k})-\displaystyle\frac{4}{k}>0\)
(ii)軸 \(\displaystyle\frac{1}{2}\sqrt{1+\displaystyle\frac{2}{k}}>0\)
(iii)端点 \(0-0+\displaystyle\frac{1}{k}>0\)
(ii),(iii)は\(k>0\)より成り立つので
(i)より
\(\displaystyle\frac{2}{k}<1\)
したがって \(k>2\)
(参考)
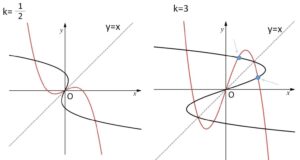
\(k=\displaystyle\frac{1}{2}\) (例題の条件に合わない) と \(k=3\) のグラフは次の通りです。
\(y=x\) 上にない交点は、1つの曲線自身で\(y=x\)について対称になっています。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→合成関数の性質 back→逆関数ともとの関数のグラフの共有点①