合成関数に関する基礎的な例題です。
(例題1)
\(f(x)=\begin{eqnarray} \left\{ \begin{array}{l} 2x+1 \quad (-1≦x≦0) \\ -2x+1 \quad (0≦x≦1) \end{array} \right. \end{eqnarray}\)
について
(1)\(y=(f \circ f)(x)\) のグラフをかけ。
(2)\((f \circ f)(a)=f(a)\) となる\(a\)の値を求めよ。
(解答)
(1)
よってまず \(-1≦f(x)≦0\) と \(0≦f(x)≦1\) で場合分けします。
\(f(x)=2x+1\) (\(-1≦x≦0\)) について (内側がこれになる)
(i)\(-1≦x≦-\displaystyle\frac{1}{2}\) のとき
\(-1≦f(x)≦0\)
このとき
\((f \circ f)(x)=2(2x+1)+1=4x+3\)
(ii)\(-\displaystyle\frac{1}{2}≦x≦0\) のとき
\(0≦f(x)≦1\)
このとき
\((f \circ f)(x)=-2(2x+1)+1=-4x-1\)
\(f(x)=-2x+1\) (\(0≦x≦1\)) について (内側がこれになる)
(iii)\(0≦x≦\displaystyle\frac{1}{2}\) のとき
\(0≦f(x)≦1\)
このとき
\((f \circ f)(x)=-2(-2x+1)+1=4x-1\)
(iv)\(\displaystyle\frac{1}{2}≦x≦1\) のとき
\(-1≦f(x)≦0\)
このとき
\((f \circ f)(x)=2(-2x+1)+1=-4x+3\)
よってグラフは次の通り。
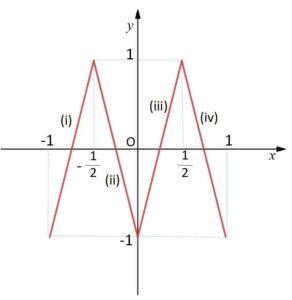
(2)
\(y=f(x)\) と \(y=(f \circ f)(x)\) のグラフの交点の\(x\)座標を求めればよい。
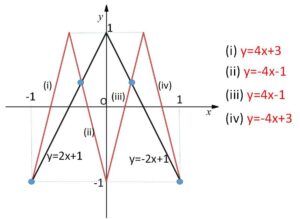
図より交点は4つ。そのうち2つの\(x\)座標は
\(x=±1\)
残りの2点については
\(2x+1=-4x-1\) より
\(x=-\displaystyle\frac{1}{3}\)
\(-2x+1=4x-1\) より
\(x=\displaystyle\frac{1}{3}\)
したがって
\((f \circ f)(a)=f(a)\) となる\(a\)の値は
\(a=±1,±\displaystyle\frac{1}{3}\)
(例題2)
関数 \(f(x)=x+5\), \(g(x)\) について \(g(f(x))=2x+3\)
が成り立つ。\(g(x)\)を求めよ。
この定理を使うときは逆関数が存在するという条件が必要ですが、どのみち逆関数の式が最後に必要になってくるので最初に求めておきます。(求まるなら存在するということ)
または、\(y=f(x)\) とおいて \(g(y)\) を求める方法もあります。
(解答)
\(f(x)=y=x+5\) について
\(x=y-5\)
\(x,y\)を入れ替えると\(f(x)\)の逆関数は
\(f^{-1}(x)=x-5\)
よって
\(g(f(x))=2x+3\) で \(x=f^{-1}(x)\) を代入して
\(g(x)=2f^{-1}(x)+3\)
\(=2(x-5)+3\)
\(=2x-7\)
(別解)
\(y=f(x)=x+5\) とおくと
\(x=y-5\)
よって \(g(f(x))=2x+3\) より
\(g(y)=2(y-5)+3=2y-7\)
変数を\(x\)にして
\(g(x)=2x-7\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→合成関数に関する例題②(分数関数・2次関数) back→合成関数の性質