順列(円順列)を利用して確率を求める問題を見ていきます。
(例題1)
男子6人、女子3人が1列に並ぶとき、次の確率を求めよ。
(1)特定の男女1組が隣り合う確率
(2)どの女子も隣り合わない確率
(解答)
(1)
特定の男女をABとして、ABひとかたまりと残り7人の計8人の順列を考えます。
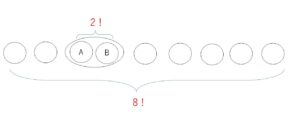

起こりうる場合の数は、\(9!\) 通り
このうち特定の男女が隣り合う並び方は、特定の男女AB1組を1人とみて計8人を並べる方法を考えると,ABの並び方も考慮して\(8!×2!\) 通り
よって求める確率は
\(\displaystyle\frac{8!×2!}{9!}=\)\(\displaystyle\frac{2}{9}\)
このうち特定の男女が隣り合う並び方は、特定の男女AB1組を1人とみて計8人を並べる方法を考えると,ABの並び方も考慮して\(8!×2!\) 通り
よって求める確率は
\(\displaystyle\frac{8!×2!}{9!}=\)\(\displaystyle\frac{2}{9}\)
(2)
男子をまず並べ、間と両端に女子を入れます。
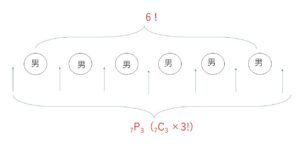

起こりうる場合の数は、\(9!\) 通り
このうちどの女子も隣り合わない場合は、まず男子6人を並べ、男子の間と両端合計7か所から3か所選んで女子を並べる方法を考えて、
\(6!×{}_7\mathrm{P}_3\) 通り
よって求める確率は
このうちどの女子も隣り合わない場合は、まず男子6人を並べ、男子の間と両端合計7か所から3か所選んで女子を並べる方法を考えて、
\(6!×{}_7\mathrm{P}_3\) 通り
よって求める確率は
\(\displaystyle\frac{6!×{}_7\mathrm{P}_3}{9!}=\)\(\displaystyle\frac{5}{12}\)
(例題2)
両親と子ども5人が円形のテーブルに着くとき、両親が隣り合う確率を求めよ。
(解答)
先ほどと同様に両親をひとかたまりとします。
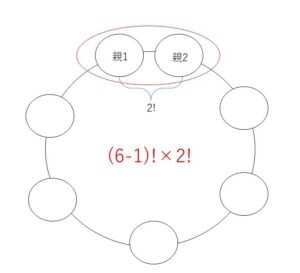

起こりうる場合の数は、\((7-1)!=6!\) 通り
このうち両親が隣り合う場合の数は、両親1組を1人として6人の円順列を考える。
両親2人の並びかたも考慮すると \((6-1)!×2!=5!×2\) 通り
よって求める確率は
\(\displaystyle\frac{5!×2}{6!}=\)\(\displaystyle\frac{1}{3}\)
このうち両親が隣り合う場合の数は、両親1組を1人として6人の円順列を考える。
両親2人の並びかたも考慮すると \((6-1)!×2!=5!×2\) 通り
よって求める確率は
\(\displaystyle\frac{5!×2}{6!}=\)\(\displaystyle\frac{1}{3}\)
以上になります。 お疲れさまでした。
ここまで見ていただきありがとうございました。