次の問題について考えていきます。(同じものを含む順列に関する問題です)
(例題)
NAGASAKIの8文字を1列に並べるとき、次の確率を求めよ。
(1)両端に母音がくる確率
(2)子音が隣り合わない確率
まず原則通り\(A\)3つを異なる文字として扱います。
(1)
\(A\)3つを異なる文字、\(A_1,A_2,A_3\) とする。
母音は、\(A_1,A_2,A_3,I\)で、子音は、\(N,G,S,K\)である。
\(A\)3つを異なる文字、\(A_1,A_2,A_3\) とする。
母音は、\(A_1,A_2,A_3,I\)で、子音は、\(N,G,S,K\)である。
8文字全部の並べ方は、\(8!\) 通り。
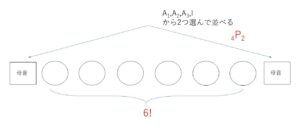
このうち両端に母音がくる並べ方は、4つの母音から2つ選んで両端に並べ、残り6文字を内側で並べる方法を考えて
\({}_4\mathrm{P}_2×6!\) 通り。
よって、求める確率は
\(\displaystyle\frac{{}_4\mathrm{P}_2×6!}{8!}=\)\(\displaystyle\frac{3}{14}\)
このうち両端に母音がくる並べ方は、4つの母音から2つ選んで両端に並べ、残り6文字を内側で並べる方法を考えて
\({}_4\mathrm{P}_2×6!\) 通り。
よって、求める確率は
\(\displaystyle\frac{{}_4\mathrm{P}_2×6!}{8!}=\)\(\displaystyle\frac{3}{14}\)
(2)
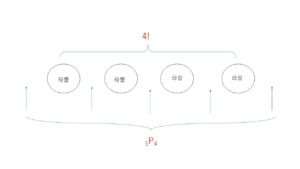
子音が隣り合わない方法は、まず母音4つを並べ、両端と母音の間の5か所から4か所選んで、子音を並べる方法を考えればよく、\(4!×{}_5\mathrm{P}_4\) 通り。
よって求める確率は
\(\displaystyle\frac{4!×{}_5\mathrm{P}_4}{8!}=\)\(\displaystyle\frac{1}{14}\)
子音が隣り合わない方法は、まず母音4つを並べ、両端と母音の間の5か所から4か所選んで、子音を並べる方法を考えればよく、\(4!×{}_5\mathrm{P}_4\) 通り。
よって求める確率は
\(\displaystyle\frac{4!×{}_5\mathrm{P}_4}{8!}=\)\(\displaystyle\frac{1}{14}\)
同じものを区別して考えると、以上のような解答になりますが、実はこの問題は同じものを区別しなくても(A3つを同じものとしても)、解くことができます。理由は後で説明します。
(別解)
(1)
(1)
8文字の並べ方は、\(\displaystyle\frac{8!}{3!}\) 通り
母音が両端にくる場合は
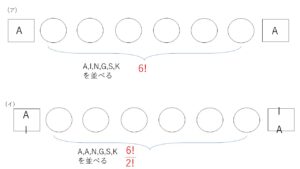
(ア)両端にAがくるとき、内側の6文字は全部異なる文字だから、\(6!\) 通り
(イ)両端にAとIがくるとき、内側の6文字には同じ文字Aが2つあり、両端AとIの並び方も考えると、\(\displaystyle\frac{6!}{2!}×2!\)\(=6!\) 通り
よって、求める確率は
\((6!+6!)÷\displaystyle\frac{8!}{3!}=\)\(\displaystyle\frac{3}{14}\)
\((6!+6!)÷\displaystyle\frac{8!}{3!}=\)\(\displaystyle\frac{3}{14}\)
(2)
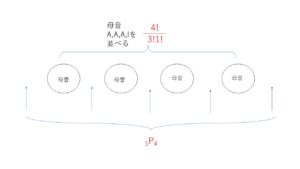
母音A,A,A,Iを並べ、その間と両端5か所から4つを選び子音を並べる方法を考えると
\(\displaystyle\frac{4!}{3!1!}×{}_5\mathrm{P}_4\) 通り
母音A,A,A,Iを並べ、その間と両端5か所から4つを選び子音を並べる方法を考えると
\(\displaystyle\frac{4!}{3!1!}×{}_5\mathrm{P}_4\) 通り
よって、求める確率は
\(\displaystyle\frac{4!}{3!1!}×{}_5\mathrm{P}_4÷\displaystyle\frac{8!}{3!}=\)\(\displaystyle\frac{1}{14}\)
\(\displaystyle\frac{4!}{3!1!}×{}_5\mathrm{P}_4÷\displaystyle\frac{8!}{3!}=\)\(\displaystyle\frac{1}{14}\)
Aを区別しない8文字の並べ方は、\(\displaystyle\frac{8!}{3!}\) 通りですが、このうちの一つ例えば NAGASAKI のA3つを区別すると、NAGASAKIという列1つに対して、3!通りの並び方があります。他の並び方でも同様にAを区別すると3!通りの並び方があり、この3!通りの並びかたそれぞれは同様に確からしいので、区別をなくした列に関しても同様に確からしいことになります。
同様に確からしく起こる事象の全体を標本空間といいます。この別解では、Aを区別していた標本空間から区別をなくした標本空間へと変えたことになります。
標本空間の取り方を変えることで計算がずっと楽になる(考え方も楽になる)場合があります。
標本空間の取り方を変えることで計算がずっと楽になる(考え方も楽になる)場合があります。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。