余事象の確率 | 教えて数学理科

余事象の確率は、確率の分野の中での重要なテーマの1つです。
まずその性質から見ていきます。

・余事象の確率
全事象\(U\)の中の事象\(A\)に対して\(A\)が起こらないという事象を\(A\)の余事象といい、\(\overline A\)で表します。余事象\(\overline A\)は\(U\)の部分集合\(A\)の補集合\(\overline A\)で表されます。

サイコロを1回投げる試行において「4の目が出る」という事象を\(A\)とします。この余事象\(\overline A\) は「4の目が出ない」という事象になりますが、それは集合で表すと、\(\overline A=\{1,2,3,5,6\}\) であり、\(A\)の補集合となります。

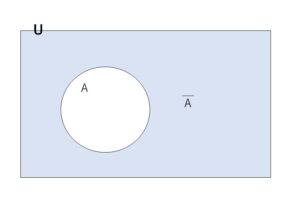
事象\(A\)と余事象\(\overline A\)について、\(A \cap \overline A=φ\) だから
\(A\)と\(\overline A\)は排反となり、確率の加法定理より

\(P(A \cup \overline A)=P(A)+P(\overline A)\)

また、\(P(A \cup \overline A)=P(U)=1\) より

\(1=P(A)+P(\overline A)\)

となり、これを変形すると

\(P(\overline A)=1-P(A)\) 　(\(P(A)=1-P(\overline A)\))

Aが起こらない確率は、全体の確率1からAが起こる確率を除くことになります。
\(P(A)=1-P(\overline A)\) という式は、Aが起こる確率を直接求めるよりも、Aが起こらない確率を求めるほうが楽な場合に使います。

(例題)
サイコロを3回投げるとき次の確率を求めよ。
(1)1の目が少なくとも1回出る確率

出た目の全部を掛けて得られる数を\(X\)とするとき
(2)\(X>2\) となる確率
(3)\(X\) が\(5\)の倍数となる確率

(解答)
(1)

直接求めると、
①1の目が1回出る　②1の目が2回出る　③1の目が3回出る
となり面倒です。なので1の目が1回も出ない確率を求めて、全体から除きます。
この問題のように「少なくとも」という文言は余事象を利用する目安となります。

全事象は \(6^3=216\) (通り)
「1の目が少なくとも1回出る」という事象を\(A\)とすると、その余事象\(\overline A\) は「1の目が1回も出ない」という事象となる。
よって、2,3,4,5,6の目だけ出る確率を考えて
\(P(\overline A)=\displaystyle\frac{5^3}{216}=\displaystyle\frac{125}{216}\)

したがって
\(P(A)=1-P(\overline A)=1-\displaystyle\frac{125}{216}=\)\(\displaystyle\frac{91}{216}\)

(2)

直接求めると
\(X=3,4,5,6,8・・・180,216\)
の場合を考えることになり大変です。よって(2)も余事象を考えます。

\(X>2\) となる事象を\(B\)とすると、\(\overline B\)は \(X≦2\) となる事象である。よって \(X≦2\) となるサイコロの目の組み合わせは
\((1,1,1),(1,1,2)\) だから、\(X≦2\) となる場合は、全部で \(1+1×3=4\) (通り)
したがって
\(P(B)=1-P(\overline B)=1-\displaystyle\frac{4}{216}=\)\(\displaystyle\frac{53}{54}\)

(3)

\(X\)が5の倍数ということは、サイコロを3回投げたうち、5が少なくとも1回出るということです。今回も余事象を考えます。

「少なくとも5が1回出る」という事象を\(C\)とすると、\(\overline C\) は「1回も5の目がでない」という事象になる。
事象\(\overline C\)は、1,2,3,4,6の目が出ることを考えると、\(5^3\)通りあり、求める確率は\(P(C)\) だから
\(P(C)=1-P(\overline C)=1-\displaystyle\frac{125}{216}=\)\(\displaystyle\frac{91}{216}\)

以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。

→高校数学TOP　next→和事象・余事象の確率とド・モルガンの法則　 back→基本性質・加法定理・和事象の確率