今度は座標平面上を動く2点の出会う確率についての問題を見ていきます。
(例題)
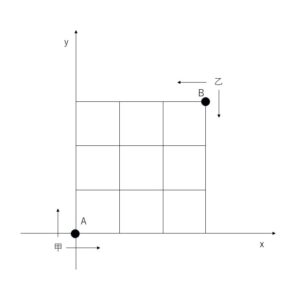
図のような格子状道路があり、ある時刻に甲はA地点\((0,0)\)に、乙はB地点\((3,3)\)にいる。甲が1秒毎に上隣の地点(道路の交点)に移動する確率を\(\displaystyle\frac{1}{2}\)、右隣の地点に移動する確率を\(\displaystyle\frac{1}{2}\)とする。また乙は1秒毎に確率\(\displaystyle\frac{1}{2}\)で左隣の地点に、確率\(\displaystyle\frac{1}{2}\)で下隣の地点に移動する。
(1)甲が地点\((k,3-k)\) (\(0≦k≦3\)) を通る確率\(p_k\)を求めよ。
(2)2人がどこかで出会う確率を求めよ。
(解答)
(1)
ある\(k\)における確率\(p_k\)を求めることになるので、答えは\(k\)を使った式となります。
\((k,3-k)\)を通るので、「右に\(k\)回、上に\(3-k\)回」移動することになり、合計で\(k+(3-k)=3\) なので、3秒後に\((k,3-k)\)を通ります。
3秒間で「右に\(k\)回、上に\(3-k\)回」移動する方法は、「→\(k\)個と↑\(3-k\)個の並べ方」を考えて、全部で\({}_3\mathrm{C}_k\)通りで、各確率は\((\displaystyle\frac{1}{2})^k(\displaystyle\frac{1}{2})^{3-k}\) となります。
ちなみに、\((k,3-k)\)は3秒後に通る点なので、次の図のC,D,E,Fのいずれかになります。これらは\(x+y=3\)上の点ですが、この式に\((k,3-k)\)を代入すると成り立つことになります。
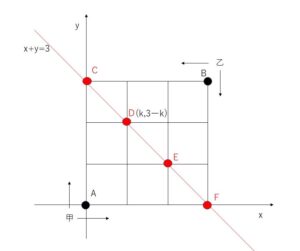
\((k,3-k)\)を通るので、「右に\(k\)回、上に\(3-k\)回」移動することになり、合計で\(k+(3-k)=3\) なので、3秒後に\((k,3-k)\)を通ります。
3秒間で「右に\(k\)回、上に\(3-k\)回」移動する方法は、「→\(k\)個と↑\(3-k\)個の並べ方」を考えて、全部で\({}_3\mathrm{C}_k\)通りで、各確率は\((\displaystyle\frac{1}{2})^k(\displaystyle\frac{1}{2})^{3-k}\) となります。
ちなみに、\((k,3-k)\)は3秒後に通る点なので、次の図のC,D,E,Fのいずれかになります。これらは\(x+y=3\)上の点ですが、この式に\((k,3-k)\)を代入すると成り立つことになります。

\((k,3-k)\)を通るのは、「右に\(k\)回、上に\(3-k\)回」移動するときなので、3秒後である。「→」\(k\)個と、「↑」\(3-k\)個、合計3個の矢印の並べ方を考えると、求める確率\(p_k\)は、
\({}_3\mathrm{C}_k(\displaystyle\frac{1}{2})^k(\displaystyle\frac{1}{2})^{3-k}=\)\(\displaystyle\frac{{}_3\mathrm{C}_k}{8}\)
\({}_3\mathrm{C}_k(\displaystyle\frac{1}{2})^k(\displaystyle\frac{1}{2})^{3-k}=\)\(\displaystyle\frac{{}_3\mathrm{C}_k}{8}\)
(2)
乙も3秒後には、C,D,E,Fの点のどれかを通ることになるので、出会うとしたら、このいずれかとなります。
では、乙が\((k,3-k)\)を通る確率ですが、最初\((3,3)\)にいるので、
「左に\(3-k\)回、下に\(k\)回」移動することになるので、(1)の甲のときと同じになります。例えば図のDに着目すると、乙と甲の移動が対称的になっていることからも分かります。
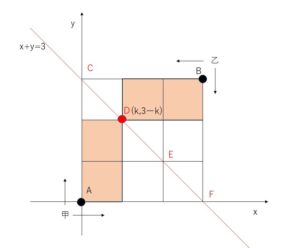
では、乙が\((k,3-k)\)を通る確率ですが、最初\((3,3)\)にいるので、
「左に\(3-k\)回、下に\(k\)回」移動することになるので、(1)の甲のときと同じになります。例えば図のDに着目すると、乙と甲の移動が対称的になっていることからも分かります。

2人が\((k,3-k)\)で出会う確率が、\(p_k×p_k\) となるので、あとはこれを\(k=0,1,2,3\)で動かして和をとれば求める確率(C,D,E,Fのどれかで出会う確率)
が求まります。
2人が出会うとすると、\(x+y=3\)上の点のいずれかで出会うことになる。
乙が\((k,3-k)\)を通る確率は、「左に\(3-k\)回、下に\(k\)回」移動することになるので、(1)の\(p_k\)と同じ。よって、\((k,3-k)\)で2人が出会う確率は
\((p_k)^2=(\displaystyle\frac{{}_3\mathrm{C}_k}{8})^2\)
乙が\((k,3-k)\)を通る確率は、「左に\(3-k\)回、下に\(k\)回」移動することになるので、(1)の\(p_k\)と同じ。よって、\((k,3-k)\)で2人が出会う確率は
\((p_k)^2=(\displaystyle\frac{{}_3\mathrm{C}_k}{8})^2\)
求める確率は、\(k=0,1,2,3\) としたときの和を求めると
\(\displaystyle\frac{({}_3\mathrm{C}_0)^2+({}_3\mathrm{C}_1)^2+({}_3\mathrm{C}_2)^2+({}_3\mathrm{C}_3)^2}{64}\)
\(=\)\(\displaystyle\frac{5}{16}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。