条件付き確率 | 教えて数学理科

条件つき確率を理解するために、次の例について考えていきます。

・条件付き確率
袋の中に、赤または白に着色したプラスチック製の玉と木製の玉が、次の表のように合わせて50個入っているとします。

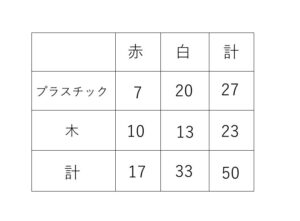
条件付き確率　表

試行「袋の中から1個玉を取り出す」
事象A「玉が赤色である」
事象B「玉がプラスチック製である」

とします。

このとき、事象Bの確率は
\(P(B)=\displaystyle\frac{27}{50}\)
となります。

ここで、取り出した玉が「赤色である」ことが分かったならば、その玉がプラスチック製である確率は、赤色の玉が\(17\)個あることから
\(p=\displaystyle\frac{7}{17}\)
となります。
この\(p\)は、事象Aが起こった(赤色の玉が取り出された)ときの、事象B(プラスチックの玉が取り出された)が起こる確率と考えることができ、これを、事象Aが起こったときの事象Bが起こる条件つき確率といい、\(p=\)\(P_A(B)\) で表します。

この例では、\(P_A(B)=\displaystyle\frac{7}{17}\) ということになりますが、
\(n(A)=17\),　\(n(A \cap B)=7\)
なので、\(P_A(B)\)を次のように表すことができます。

\(P_A(B)=\displaystyle\frac{n(A \cap B)}{n(A)}\)・・・①

①の右辺より、条件付き確率\(P_A(B)\)は、全事象を\(A\)とみなしたときの、積事象\(A \cap B\) の確率と考えることができます。

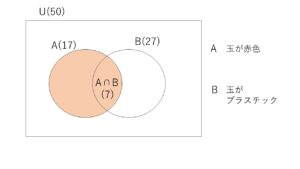
条件付き確率　ベン図

また、①の右辺の分母分子を全事象\(U\)の起こる場合の数\(n(U)(≠0)\)で割ることで

\(P_A(B)=\displaystyle\frac{P(A \cap B)}{P(A)}\)・・・②

が得られます。

事象Aが起こったときの事象Bが起こる、条件付き確率\(P_A(B)\)は

\(P_A(B)=\displaystyle\frac{n(A \cap B)}{n(A)}\)　(\(n(A)≠0\))
\(P_A(B)=\displaystyle\frac{P(A \cap B)}{P(A)}\)　(\(P(A)≠0\))

・\(P_A(B)\) と \(P(A \cap B)\) の違い
例えばくじを引いたときの当たる確率は、くじを引くときの当たる確率であって、実際にはくじを引いていない場合に、どれくらい当たるのかを数値化したものです。このように、条件つき確率ではない通常の確率では、何も起きていないときに、ある事象が起こる割合を考えています。 \(P(A \cap B)\)は言葉で表すと、「AかつBが起こる確率」ですが、\(A\)も\(B\)も起きていません。

天気予報は、出かける前にどれくらいの確率で雨が降るか(未来の雨の降る可能性)を知ることに意味があるわけで、1日が終わって帰ってきたときに、「今日は雨でした、傘を持って行ったほうがよかったですね」と言われても仕方がないですよね。

これに対して条件付き確率は、ある事象がすでに起きてしまっている場合の確率を考えています。\(P_A(B)\)は言葉で表すと「Aが起こった時のBが起こる確率」ですが、Aはすでに起きてしまっています。Aがすでに起きている場合でBが起こる確率を考えるわけです。

条件つき確率にも意味はあります。→(4-5)原因の確率　で一番実感しやすいと思います。

・\(P_A(B)\) と \(P(B)\) の関係
例でもわかるように、一般的には \(P_A(B)=P(B)\) とはなりません。 (\(P_A(B)=P(B)\)となることもあります)
\(P(B)=\displaystyle\frac{27}{50}\) →　\(P_A(B)=\displaystyle\frac{7}{17}\)
のように、Bが起こる確率は、Aが起こることによって変化しています。

例えば、あなたを含む10人に1億円をもらえるチャンスが与えられて、10人のうちの1人が必ずもらえるとします(確率は平等)。
まだ何も起きていない(何もわかっていない)状態では、10人それぞれの1億円をもらえる確率は \(\displaystyle\frac{1}{10}\) ですが、他の9人全員が非当選となった(非当選であることを知った)とすると、確率1であなたが1億円をもらえることになります。このように後の出来事や情報の入手で確率は変化しています。
もちろん変わらない場合もあります。今の例でいうと、まだ全員にチャンスがあるときに、たとえば偶然くしゃみをしたとしても、当たる確率は変わりませんね。
詳しくは数Bでやります。

(例題1)
白玉が3個、赤玉が5個入った袋がある。この袋の中から玉を袋に戻さないで1つずつ2個取り出すとき、最初の玉が白である事象をA、2番目の玉が赤である事象をBとする。
\(P_A(B)\) を求めよ。

(解答1)
\(P_A(B)=\displaystyle\frac{n(A \cap B)}{n(A)}\) を用いた方法

\(n(A)\) は、1回目に白玉が出て、2回目には何が出てもよい場合の数なので
\(n(A)=3×7=21\)

\(n(A \cap B)\)は、1回目に白玉が出て、2回目には赤玉が出る場合の数なので
\(n(A \cap B)=3×5=15\)

よって

\(P_(B)=\displaystyle\frac{15}{21}=\)\(\displaystyle\frac{5}{7}\)

(解答2)

\(P_A(B)=\displaystyle\frac{P(A \cap B)}{P(A)}\) を用いた方法

\(P(A)\)は、1回目に白玉が出る確率なので
\(P(A)=\displaystyle\frac{3}{8}\)

\(P(A \cap B)\)は、1回目に白玉が出て、2回目には赤玉が出る確率なので
\(P(A \cap B)=\displaystyle\frac{3×5}{8×7}=\displaystyle\frac{15}{56}\)

よって
\(P_A(B)=\displaystyle\frac{15}{56}÷\displaystyle\frac{3}{8}=\)\(\displaystyle\frac{5}{7}\)

(解答3)

\(P_A(B)\)の意味を考える方法

\(P_A(B)\)は、1回目に白玉が出た(白玉が出るという事象が起こった)ときの、2回目に赤玉が出る確率である。1回目に白玉が出たとき、袋の中には、白玉2個と赤玉5個が残っているので

\(P_A(B)=\)\(\displaystyle\frac{5}{7}\)

(解答3)の方法は、この例題のように問題で問われている条件付き確率の意味が明らかに分かる場合に使ってください。
問題文の条件付き確率の意味がはっきりとしない場合には、(解答1,2)の方法を用いてください。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。

→高校数学TOP　next→確率の乗法定理　 back→確率の最大値